Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 13.Problemas - Ex. 71
71 - Reconsidere Prob. 13-70. Usando o software EES (ou outro), investigue os efeitos do diâmetro do cilindro externo e da emissividade do escudo de radiação sobre a taxa líquida de transferência de calor por radiação entre os dois cilindros. Deixe o diâmetro variar de a e a emissividade de a . Trace a taxa de transferência de calor por radiação em função do diâmetro e da emissividade e discutir os resultados.
Passo 1
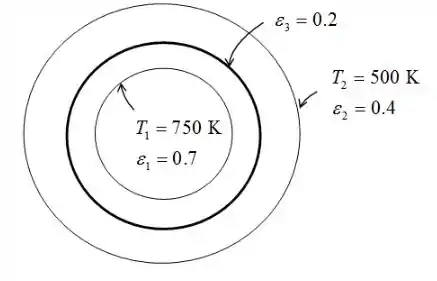
Dados fornecidos:
Diâmetro do cilindro interno,
Diâmetro do cilindro externo,
Emissividade do cilindro interno,
Emissividade do cilindro externo,
Temperatura do cilindro interno,
Temperatura do cilindro externo,
Diâmetro da blindagem de radiação coaxial,
Emissividade do escudo de radiação,
Passo 2
Considerações:
1. As superfícies são difusas, cinza e opacas
2. Existem condições operacionais estáveis
3. A transferência de calor de e para as superfícies é devida apenas à radiação
Passo 3
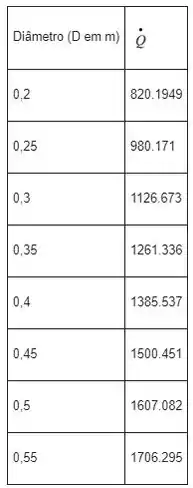
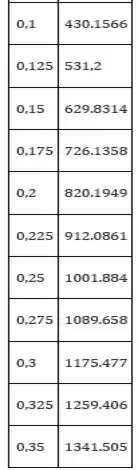
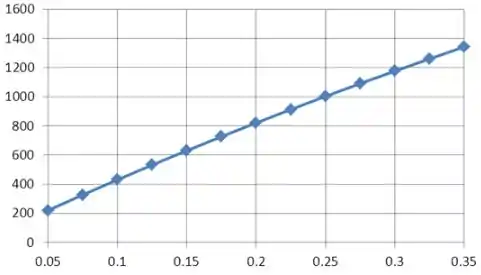
A variação da transferência de calor por radiação varia o diâmetro do escudo.
A taxa líquida de transferência de calor por radiação entre os dois cilindros com blindagem por unidade de comprimento pode ser expressa como:
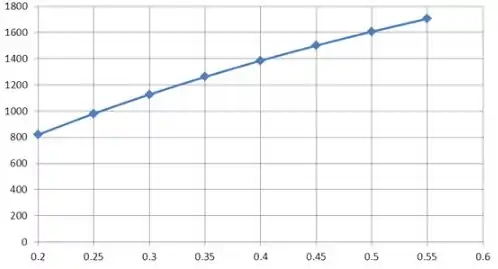
A equação acima é resolvida variando o diâmetro da blindagem, os valores correspondentes da taxa de transferência de calor por radiação são tabulados e plotados conforme mostrado abaixo.
O gráfico abaixo é dado pela variação da emissividade pelo diâmetro.
Passo 4
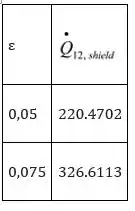
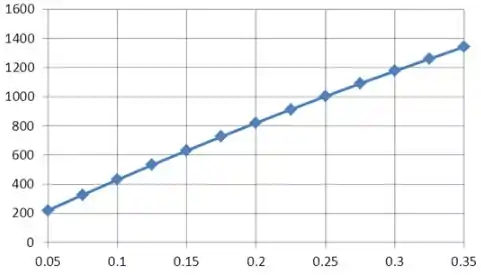
A variação da transferência de calor por radiação varia a emissividade da blindagem.
A taxa líquida de transferência de calor por radiação entre os dois cilindros com blindagem por unidade de comprimento pode ser expressa como:
A equação acima é resolvida variando a emissividade da blindagem, os valores correspondentes da taxa de transferência de calor por radiação são tabulados e plotados conforme mostrado abaixo:
Resposta
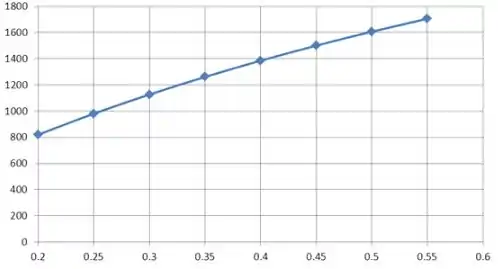
Diâmetro
Emissividade