Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 8.Problemas - Ex. 57

Refrigerante-134a é transportado a 0,1 kg/s através de um tubo de Teflon com diâmetro interno Di = 25 mm e diâmetro externo De = 28 mm, enquanto ar atmosférico a V = 25 m/s e 300 K escoa em escoamento cruzado sobre o tubo. Qual é a taxa de transferência de calor para o Refrigerante-134a a 240 K, por unidade de comprimento do tubo?

Passo 1

Vamo analisar o enunciado junto pra entender o que ele quer de você.

Temos um tubo por onde escoa Refrigerante-134a a 240   K escoando a 0,1   k g / s , ao mesmo tempo que está exposto à convecção de ar, como demonstra o esquema ilustrativo abaixo, onde já estão demonstradas todas as grandezas que iremos usar ao longo da questão:

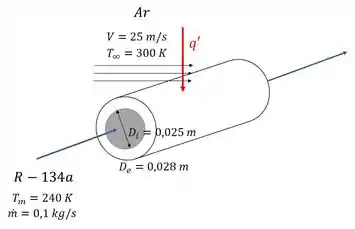
A questão quer que a gente calcule a taxa de calor por unidade de comprimento do tubo q ' , a partir da equação:

q ' =   T ∞ - T m R t '

Sendo R t ' a resistência térmica por unidade de comprimento.

Para calcular a resistência térmica, devemos analisar o circuito térmico para esse volume de controle, dado na figura abaixo:

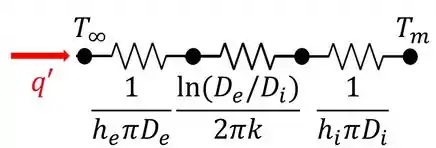
Ou seja, a transferência de calor se dá do ar externo ao tubo até o seio do Refrigerante-134a, passando por duas resistências convectivas e uma condutiva.

Dessa maneira, a resistência térmica é calculada da seguinte forma:

R t ' =   1 h e π D e + l n ⁡ ( D e / D i ) 2 π k + 1 h i π D i

Pra gente resolver a questão, vamo precisar procurar as propriedades do R-134a, do Teflon e do ar.

Para o ar a 300   K , vamos na Tabela A.4 (página 634), temos as seguintes propriedades:

k   =   0,0263 W m . K ν = 15,89 x 10 - 6   m ² s P r   =   0,707

Para o R-134a a 24 0   K , vamos na Tabela A.5 (página 638), temos as seguintes propriedades:

k   =   0 , 1073 W m . K μ = 4,202 x 10 - 4   N . s m ² P r   =   5,0

E por fim, para o Teflon a uma aproximação a 300   K , indo na Tabela A.3 (página 629), k =   0 , 35 W / m ⋅ K .

Agora a gente pode ir resolver a questão no próximo passo.

Passo 2

Para calcular a resistência térmica, precisamos antes calcular os coeficientes de transferência de calor h i e h e   a partir da equação:

h =   k D N u D

Vamos dividir os cálculos em escoamento interno e externo.

  1. Escoamento interno

    2. Pro escoamento interno, vamos calcular o número de Reynolds:

    R e D , i = 4 m ˙ π D i μ = 4 0,1 k g s π 0,025   m 4,202 x 10 - 4   N . s m ² = 12 12 0

    Ou seja, temos aqui um escoamento turbulento. Sendo assim, a correlação pra calcular número de Nusselt é:

    N u D , i =   0,023 R e D , i 4 / 5 P r 0,4

    Sendo assim, o coeficiente de transferência de calor pode ser calculado como:

    h i =   k D i 0,023 R e D , i 4 / 5 P r 0,4 =     0 , 1073 W m . K 0,025   m 0,023 12120 4 / 5 5,0 0,4 = 347 , 3 6 W m 2 . K

  2. Escoamento externo ao cilindro

Vamos calcular o número de Reynolds:

R e D , e = V D e ν = 25 m s 0,028   m 15,89 x 10 - 6   m ² s = 4,4 x 10 4

Ou seja, temos aqui um escoamento turbulento. Sendo assim, a correlação pra calcular número de Nusselt é a correlação de Zukauskas, com as constantes devidamente já substituídas:

N u D , e =   0 , 26 R e D , e 0,6 P r 0,37

Sendo assim, o coeficiente de transferência de calor pode ser calculado como:

h e =   k D e   0 , 26 R e D , e 0,6 P r 0,37 =     0,0263 W m . K 0,028   m 0 , 26 4,4 x 10 4 0,6 0,707 0,37 = 131 W m 2 . K

Passo 3

Agora, pra finalizar a questão, vamo calcular o taxa de calor por unidade de comprimento do tubo:

q ' =   T ∞ - T m 1 h e π D e + l n ⁡ ( D e / D i ) 2 π k + 1 h i π D i

→ q ' = 300   K - 240   K   1 131 W m 2 . K π 0,028   m + l n ⁡ ( 0,028 / 0,025 ) 2 π 0 , 35 W m . k 1 347,36 W m 2 . K π 0,025   m

→ q ' = 342,84   W / m

Pronto, matamos a questão juntos!

Resposta

O coeficiente de transferência de calor por unidade de comprimento é q ' = 342,84   W / m .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

NaK (45%/55%), que é uma liga de sódio e potássio, é usada para resfriar reatores nucleares de nêutrons rápidos. O NaK escoa a uma vazão de 0,8k g / s através de um tubo com diâmetro D=40m m , que tem
Para as condições do Problema 8.70, qual deve ser o comprimento da região anular se a vazão da água for de 0,35k g / s ao invés dos 0,02k g / s ?
Um gás ideal escoa no interior de um tubo de pequeno diâmetro. Deduza uma expressão para a densidade (massa específica) de transição do gás,ρ c , abaixo da qual os efeitos de microescala têm que ser l
Considere uma região anular entre dois tubos concêntricos na qual os diâmetros interno e externo são de 25m m e 50m m . Água entra na região anular a 0,0 3k g / s e 25 ° C . Se a parede do tubo intern
Ar, a 4 × 10 – 4k g / s e 20° C , entra em um duto retangular que tem 1m de comprimento e 4m m por 16m m de lado. Um fluxo térmico uniforme de 500W / m 2 é imposto na superfície do duto. Qual é a temp