Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 32

Ar, a 3   a t m   e 100 ° C , é descarregado de um compressor em um receptor vertical com   2,5   m de altura e 0,75   m de diâmetro. Suponha que a parede do receptor apresente resistência térmica desprezível, esteja a uma temperatura uniforme, e que a transferência de calor nas suas superfícies interna e externa é por convecção natural em uma placa vertical. Despreze a radiação e quaisquer perdas térmicas pela extremidade superior do receptor.

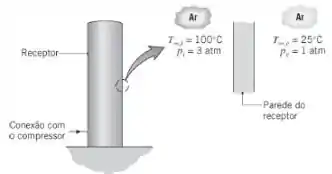
(a) Estime a temperatura da parede do receptor e a taxa de transferência de calor para o ar ambiente a 25 ° C . Para facilitar o uso das correlações de convecção natural com temperaturas do filme apropriadas, suponha que a temperatura da parede do receptor seja 60 ° C .

(b) As temperaturas do filme utilizadas na parte (a) são razoáveis? Em caso negativo, utilize um procedimento iterativo para determinar valores consistentes.

(c) Agora considere duas características do receptor que foram desprezadas na análise anterior: (i) a troca de calor por radiação saindo de sua superfície externa, que tem emissividade igual a   0,85 , para uma grande vizinhança também a 25 ° C ; e (ii) a resistência térmica de uma parede com 20   m m de espessura e condutividade térmica de 0,25   W / ( m   ·   K ) . Represente o sistema por um circuito térmico e estime as temperaturas das superfícies da parede e a taxa de transferência de calor.

Passo 1

Antes de tudo segura na minha mão e respira fundo... Eu sei que essa questão é grande mas juntos conseguimos fazer, beleza?! Vamos lá! Aqui nós temos um tanque de recebimento de ar de altura e diâmetro definidos. O ar interno é de 3   a t m   e   100 ° C enquanto o ar ambiente externo é de 25 ° C .

Com essas informações queremos encontrar a temperatura da parede do receptor e transferência de calor para o ar ambiente. E se as temperaturas de filmes encontradas não forem razoáveis devemos usar um procedimento de iteração para encontrar valores consistentes.

Passo 2

Para resolver essa questão vamos assumir:

(1) Os efeitos da radiação de superfície são desprezíveis;

(2) Perdas na parte superior e inferior do receptor são insignificantes;

(3) A resistência térmica da parede do receptor é desprezível em comparação com a resistência de convecção livre;

(4) O ar interior e exterior é quieto e extensivo.

A taxa de transferência de calor do receptor segue o circuito térmico,

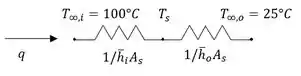
q = ∆ T R t = T ∞ , i - T ∞ , o 1 / h - o A s + 1 / h - i A s = A s ( T ∞ , i - T ∞ , o ) 1 / h - o + 1 / h - i    

Onde h - o e h - i   devem ser estimados a partir de correlações livres de convecção.

Passo 3

Devemos assumir um valor de T s para obter as primeiras estimativas para Δ T o   =   T s   - T ∞ ,   o e Δ T i   =   T ∞ ,   o   -   T s , assim como T f ,   o   e   T f ,   i . Suponhamos que T s   =   60   °   C , então,

Δ T o   =   60   –   25   =   35 ° C

  T f ,   o   =   315   K

  Δ T i   =   100   -   60   =   40   °   C

  T f ,   i   =   350   K

E,

R a L , o = g β Δ T L 3 ν α = 9,8 m s 2 1 3 15 K 35 K 2,5 m 3 1 , 74 × 10 - 5 m 2 s 2 , 472 × 10 - 5 m 2 s = 3,952 × 10 10

R a L , i = 9,8 m s 2 1 35 0 K 40 K 2,5 m 3 6,973 × 10 - 6 m 2 s 9,967 × 10 - 6 m 2 s = 2,518 × 10 1 1

Passo 4

Aproximando a parede do receptor como uma placa vertical temos,

N u L , o - = 0,825 + 0,387   3,952 × 10 10 1 6 1 + 0,492 0,70 49 9 16 8 27 2 = 390,0

N u L , i - = 0,825 + 0,387   2,518 × 10 11 1 6 1 + 0,492 0,70 0 9 16 8 27 2 = 706 , 4

E,

h L , o - = N u L , o - k L = 390,0 × 0,02 741 W m . K 2,5 m = 4,27 W m 2 . K

h L , i - = 706,4 × 0,0 30 W m . K 2,5 m = 8,48 W m 2 . K

Além disso, também temos que,

q = π × 0,75 m × 2,5 m 100 - 25 K 1 4,27 + 1 8,48 m 2 K . W   = 1225   W

Então,

T s = T ∞ , i   - q h L , i - A s = 74,9 ° C

Passo 5

A partir do resultado acima para T s , as temperaturas do filme computado são,

T f , o = 323   K e T f , i = 3 60   K

Em comparação com os valores assumidos de 315 e 350   K , respectivamente. Usando Ferramentas de Correlação IHT para Convecção Livre, Placa Vertical e o circuito térmico representando encontramos T s , em vez de usar como valor assumido,

T ∞ , o - T s 1 / h - o = T s - T ∞ , o 1 / h - o

Assim, encontramos,

q = 1262   W

T s = 71,4 ° C

Com T f ,   o   =   321 K   e 359   K . A iteração influenciou apenas ligeiramente a taxa de calor.

Resposta

  1. T s = 74,9 ° C
  2. T s = 71,4 ° C
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A placa absorvedora e a placa de cobertura adjacente em um coletor solar plano estão a 70° e 35°C, respectivamente, e encontram-se separadas por uma camada de ar com 0,05 m de espessura. Qual é a taxa
Considere um sistema de armazenamento térmico no qual o material que muda de fase (parafina) é confinado em um grande reservatório, cuja superfície inferior, horizontal, é mantida a Ts = 50°C por água
Uma cavidade retangular é formada por duas placas paralelas quadradas com 0,5 m de lado, separadas por uma distância de 50 mm. As fronteiras laterais da região entre as placas são isoladas. A placa aq
Uma chapa fina de vidro de uma janela com 1m de lado separa o ar quiescente de uma sala a T ∞ , i=20 ° C do ar ambiente externo, também quiescente, a T ∞ , e=220 ° C . As paredes da sala e a vizinhanç
Partindo da correlação de convecção natural com a forma dada pela Equação 9.24, mostre que, para o ar a pressão atmosférica e a uma temperatura do filme de 400K , o coeficiente de transferência de cal