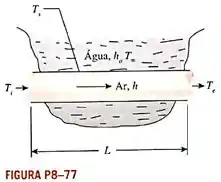
Para resfriar um armazém no verão sem usar sistema de ar condicionado convencional, o proprietário decidiu contratar um engenheiro para projetar um sistema alternativo que faça uso da água de um lago nas proximidades. O engenheiro decidiu passar o fluxo de ar através de um tubo fino liso de cobre de de diâmetro submerso no lago. A água do lago está normalmente a uma temperatura constante de , e o coeficiente de transferência de calor por convecção é Considerando que o ar entra no tubo de cobre a uma temperatura média de e a uma velocidade média de , determine o comprimento do tubo de cobre necessário de modo que a temperatura média de saída do ar seja .

Primeiro, vamos começar calculando a temperatura média do ar no tubo. Assim temos:

Aqui,  é a temperatura média do ar,  é a temperatura media do ar na entrada do tubo e  é a temperatura média do ar na saída do tubo. Substituindo os dados, temos:

Com a temperatura média, podemos obter as propriedades do ar à temperatura  e pressão de  na tabela do Apêndice A-15.

Calor específico de pressão constante:

Condutividade térmica:

Densidade:

Viscosidade cinemática:

Número de Prandtl:

Futuramente vamos precisar da vazão mássica do ar através do tubo, então, vamos calcular a vazão mássica usando a fórmula:

Aqui, é a área de fluxo do tubo e é a velocidade média do fluxo. Substituindo os termos da equação, temos:

Agora, vamos encontrar o número de Reynolds para o fluxo. Podemos usar a seguinte relação:

Aqui, é a viscosidade cinemática. Substituindo os termos da equação, temos:

Para esse processo, temos que , indicando que o fluxo totalmente turbulento.

Vamos agora calcular o número de Nusselt. Encontramos na tabela que , e como o fluxo é turbulento e , podemos usar a equação de Dittus-Boelter para encontrar o número de Nusselt. Assim temos:

Como o ar que flui pelo tubo esta sendo refrigerado, .

Substituindo os termos da equação, temos:

Com o número de Nusselt, podemos encontrar o coeficiente de transferência de calor por convecção na definição de número de Nusselt. Assim temos:

Aqui, é a condutividade térmica. Substituindo os termos da equação, temos:

Podemos aplicar a equação do balanço de energia na superfície do tubo. Onde podemos igualar a taxa de transferência de calor para a água do lago.

Com a transferência de calor para o ar:

Igualando as duas equações, temos:

Aqui, é o fluxo mássico, é o calor específico, é a temperatura do ar na entrada, é a temperatura do ar na saída, é a temperatura da agua do lago, é área da superfície do tubo e é coeficiente de transferência de calor por convecção.

Substituindo os termos pelos dados fornecidos no enunciado, temos:

Agora, vamos usar a fórmula da temperatura média do fluido na saída para encontrar o comprimento do tubo. Assim temos:

Reorganizando, temos:

Aqui  é a temperatura do fluxo de entrada,  é a temperatura da superfície do tubo,  é a temperatura do fluxo de saída,  é a área da superfície,  o coeficiente de transferência de calor e  é a vazão mássica. Temos que .

Substituindo a equação na equação encontrasdas nos passos e , temos:

Substituindo os termos pelos dados fornecidos no enunciado, temos:

Com o auxilio de uma calculadora HP, temos que a temperatura na superfície é:

Substituindo a temperatura da superfície do tubo na equação podemos encontrar o comprimento do tubo. Assim temos:

Portanto, o comprimento necessário do tubo de cobre é .