Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 183
O sistema de teste de bombas do Problema 8.128 está funcionando com uma bomba que gera uma diferença de pressão dada por , em que é dado em e a vazão gerada é em expressa em . Determine a vazão de água, a diferença de pressão e a potência de acionamento da bomba, sendo sua eficiência de 70%.
Passo 1
Vamos lá!!! Primeiramente vamos ver um esqueminha do que temos no problema :
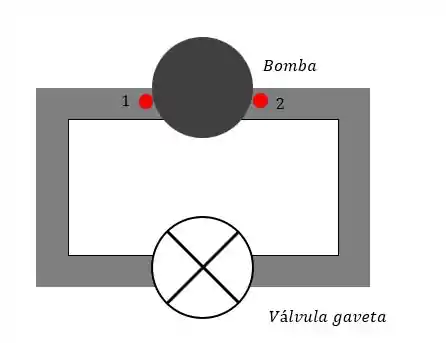
Temos a equação:
Os pontos escolhidos já estão marcados no esqueminha, eles estão na mesma altura e como temos o mesmo diâmetro a velocidade deve ser igual nos dois pontos, logo ficamos com:
Sabendo que:
E:
é calculado por:
Ou:
Temos joelhos e uma válvula gaveta, logo:
Arrumando:
Substituindo na equação de energia:
Essa é a equação do sistema!!
Passo 2
Temos no enunciado a equação da bomba:
Para descobrir a potência da bomba temos:
O problema é que não temos nenhum desses dados!!
Para resolver esse problema a gente vai pedir a ajuda do Solver que é uma ferramenta do excel!
Vamos colocar as duas equações de pressão e usar o Solver para descobrir qual é a vazão para qual as pressões calculadas por ambas equações sejam iguais!
Então bora lá! Do lado direito temos todos os dados disponíveis:
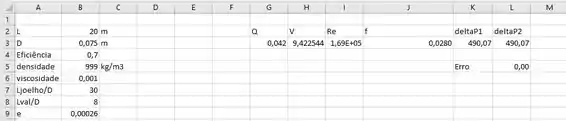
Temos então:
Passo 3
Agora só falta achar a potência:
Uhuuuul!!!