Considere o escoamento laminar completamente desenvolvido no espaço anular formado pelos dois cilindros concêntricos mostrados no diagrama do Problema 8.53, porém com gradiente de pressão, ∂p/∂x, e o cilindro interno estacionário. Seja e . Mostre que o perfil de velocidade é dado por:
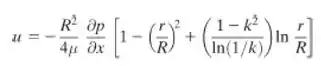
Passo 1
Navier Stokes para coordenadas cilindricas:
Nesse caso ! Vamos ver o que podemos cortar!!!
- Considerando um escoamento permante, podemos tirar a derivada em relação ao tempo;
- ;
- ;
- Se o escoamento é permantente,
- que varia apenas em , do lado direito podemos cortar tudo que tem derivada de variando com e ;
- O tubo esta deitado, então podemos cortar !
Passo 2
Agora é a vez de integrar!!! Temos:
Separando:
Aqui a gente imagina dois pontos no qual não temos os valores, mas tudo bem, ainda é verdade que no ponto , a pressão é e no ponto a pressão é , certo?
Integrando, ficamos com:
Que pode ser reescrito como:
Passo 3
Agora vamos para a segunda integração! Temos que separar de novo:
Jogando as constantes para fora e integrando:
Ficamos com:
Se tivessemos o escoamento dentro de um tubo, saberiamos que quando a derivada de seria zero, por ser um ponto onde a velocidade é máxima! Mas não é o que temos aqui!
Aqui o escoamento é no espaço anular entre dois tubos, então não temos nenhum valor para substituir e achar , portanto vamos manter e seguir em frente!
Passo 4
Vamos separar de novo:
Jogando as constantes pra fora e aplicando a integral:
Integrando:
Vamos tirar esse sinal da frente de invertendo o logaritimo, só pra ficar mais arrumadinho!!
DICA!!!!! Esse tipo de questão estamos trabalhando com muitas manipulações na expressão, então SEMPRE que for possível isolar elementos repetidos, ou simplificar a expressão faça isso! Vai facilitar a nossa vida mais pra frente e nos poupa de erros de sinais e coisas do tipo! Combinado?!
Isolando :
Passo 5
O enunciado diz que e . A velocidade nesses pontos não é dada, mas como se trata das paredes dos tubos interno e externo, pela condição de não deslizamento, sabemos que nesses pontos é igual a zero!
A primeira condição de contorno:
Vamos substituir na a expressão antes de isolarmos , porque depois podemos igualar :
A segunda condição de contorno:
Aplicando:
Igualando as duas expressões:
Jogando tudo com para a direita:
Aplicando a propriedade de subtração e divisão do logarítimo:
Finalmente isolando :
Agora vamos achar , pegando qualquer uma das condições de contorno:
Substituimos :
já esta isolado, só precisamos dar aquela ajeitadinha:
Passo 6
Substituindo e , agora a gente vai usar a expressão com o já isolado:
Viiiu como ficou grandão!! Agora imagina a confusão se não estivessemos sempre orgnizando as expressões:
Colocando termos em evidência:
Passo 7
Teroricamente acabamos, mas a expressão ainda não esta igual a do enunciado, então a gente vai dar uma brincadinha com os sinais de menos até chegarmos lá, uma das estratégias que vamos usar é:
E a outra é que:
Ficamos com:
A única coisa diferente é , mas:
Se a gente considerarmos que os pontos e estão beeeeeem pertinhos, que a distância é infinitesimal!
Logo:
Uhuuuuuul!!
Passo 8
Agora vamos oberr a expressão para a localização da velocidade máxima como uma função de k. Fazendo !
Para isso vamos pegar uma expressão onde aparece a derivada da velocidade em relação a :
Conhecemos :
Isolando a derivada:
Substituindo :
Arrumando:
Ficamos com:
Substitundo :
Arrumando:
Uhuuul!! Agoora sim!!!
Resposta
Ei, a resposta está no passo a passo :)