Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 130

Uma superfície quente a 120 ℃ deve ser resfriada fixando-se aletas do tipo pino de alumínio ( k = 237 W / m . K e α = 97,1 × 10 - 6 m 2 / s ) de 8   c m de comprimento, 0,8   c m de diâmetro, com distância de centro a centro de 1,6   c m . A temperatura do meio circundante é 15 ℃ , e o coeficiente de transferência de calor na superfície é 35   W / m ² K . Inicialmente, as aletas estão a uma temperatura uniforme de 30 ℃ e, no momento t = 0 , a temperatura da superfície quente aumenta para 120 ℃ . Pressupondo uma condução de calor unidimensional ao longo da aleta e um espaçamento nodal de ∆ x = 2   c m , com um passo de tempo de ∆ t = 0,5 s , determine as temperaturas nodais após 5 minutos, utilizando método explícito de diferenças finitas. Além disso, determine o tempo necessário para que as condições permanentes sejam alcançadas.

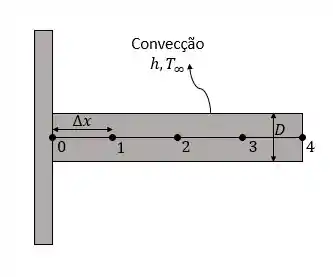
Passo 1

Primeiramente, iremos assumir algumas considerações para simplificar o problema. São elas:

  • A transferência de calor através da aleta é unidimensional.
  • Coeficiente de transferência de calor por convecção é constante e uniforme.
  • As propriedades térmicas da aleta são constantes.
  • Transferência de calor por radiação é desprezível.
  • Perda de calor da aleta é considerada.

De posse dessas características, podemos entender melhor o sistema com o qual a questão pretende trabalhar.

Passo 2

Neste problema, possuímos 5 nós, porém a temperatura da base, T 0 , é especificada, nos deixando com apenas 4 temperaturas desconhecidas, logo, precisamos de 4 equações para encontra-las. Para tal, usaremos a abordagem do balanço de energia e a formulação explícita do método das diferenças finitas, que ficarão da seguinte maneira:

Nó 1 :

h p ∆ x T ∞ -   T 1 i + k A T 2 i -   T 1 i ∆ x + k A T 0 i -   T 1 i ∆ x =   ρ A C p ∆ x T 1 i + 1 -   T 1 i ∆ t

Nó 2 :

h p ∆ x T ∞ -   T 2 i + k A T 3 i -   T 2 i ∆ x + k A T 1 i -   T 2 i ∆ x =   ρ A C p ∆ x T 2 i + 1 -   T 2 i ∆ t

Nó 3 :

h p ∆ x T ∞ -   T 3 i + k A T 4 i -   T 3 i ∆ x + k A T 2 i -   T 3 i ∆ x =   ρ A C p ∆ x T 3 i + 1 -   T 3 i ∆ t

Nó 4 :

h p ∆ x 2 + A T ∞ -   T 4 i + k A T 3 i -   T 4 i ∆ x =   ρ A C p ∆ x 2 T 4 i + 1 -   T 4 i ∆ t

Sabendo-se que A =   π D ² / 4 é a área da seção transversal e p = π D é o perímetro da aleta. Não é fornecido o valor de C p , mas α = k / ρ C p é conhecido, e nas 4 equações é possível manipular as variáveis de forma a aparecer o α .

Passo 3

Possuindo todos os dados necessários para se calcular as temperaturas em um intervalo de tempo qualquer, a questão pede para verificarmos as temperaturas no instante t = 5   m i n , e como o passo de tempo é de 0,5 s , o instante requerido é 600 vezes o passo de tempo.

Para esse instante, as temperaturas são as seguintes:

T 1 = 110,6 ℃

T 2 = 103,9 ℃

T 3 = 100 ℃

T 4 = 98,5 ℃

E a temperatura no nó 0 continua igual a 120 ℃ .

Passo 4

Para se verificar em qual instante as temperaturas atingem condições permanentes, deve-se verificar o resultado das equações variando cada unidade do intervalo de tempo. O momento em que a temperatura não apresentar mais variação, ou a variação estiver dentro de um intervalo especificado como mínimo, entende-se que as condições permanentes foram atingidas. Ao se realizar esse processo, verifica-se que as condições permanentes são atingidas quando t = 3,8   m i n ou após 456 intervalos de tempo. Aconselhável a utilização de algum software, como o Excel, para a realização do processo!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro