Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 83
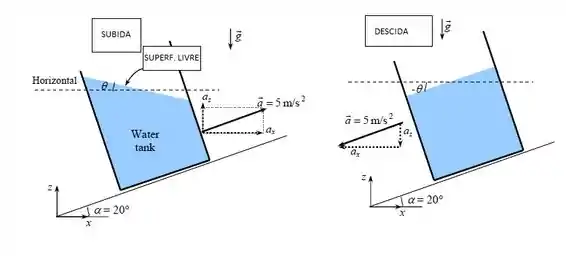
Um tanque de água está sendo rebocado em uma estrada inclinada que faz 20° com a horizontal a uma aceleração constante de 5 m/s² na direção do movimento. Determine o ângulo que a superfície livre da água faz com a horizontal. O que você responderia se a direção do movimento fosse descendente na mesma estrada com a mesma aceleração?
Passo 1
Tomando o desenho acima, podemos escrever as seguintes correlações:
Com isso podemos dizer também que:
Passo 2
Se revertermos a direção:
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Considere uma superfície circular sujeita a forças hidrostáticas por um líquido de densidade constante. Se as intensidades das componentes horizontal e vertical da força hidrostática resultante forem
Você já deve ter notado que a espessura de uma barragem é maior no fundo. Explique por que as barragens são construídas dessa forma.
Considere uma superfície curva submersa. Explique como você determinaria a componente horizontal da força hidrostática que age sobre essa superfície.
Considere um contêiner cilíndrico vertical parcialmente preenchido com água. Agora o cilindro é posto a girar com relação a seu eixo a uma velocidade angular especificada, e o movimento de corpo rígid
Uma placa retangular com 4 m de altura e 5 m de largura bloqueia a lateral de um canal de água doce com 4 m de profundidade, como mostra a Figura P3-56. A placa tem dobradiças em tomo de um eixo horiz