Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 12.Problemas - Ex. 15
Um tanque de volume contém ar comprimido a . A pressão manométrica no tanque é . Avalie o trabalho requerido para encher o tanque comprimindo ar da condição padrão por compressão isotérmica e compressão isentrópica seguida de resfriamento à pressão constante. Qual é o pico de temperatura do processo de compressão isentrópica? Calcule a energia removida durante o resfriamento para o processo. Considere comportamento de gás ideal e processos reversíveis. Marque pontos de estado em diagramas e para cada processo.
Passo 1
Iniciaremos o problema calculando a massa do tanque:
Como não possuímos a massa específica devemos calculá-la a partir da equação dos gases ideais:
A pressão no tanque é obtida por:
Sendo:
;
.
Temos:
Voltando na equação dos gases ideais.
Sendo:
;
.
Temos:
Substituindo a massa específica obtida na primeira equação apresentada e o enunciado nos dá , temos:
Passo 2
Desenhe a curva entre a entropia e a temperatura do sistema:
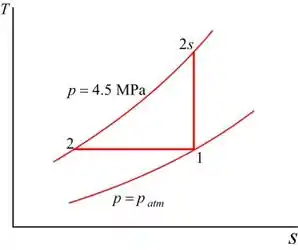
Desenhe a curva entre a pressão e o volume do sistema:
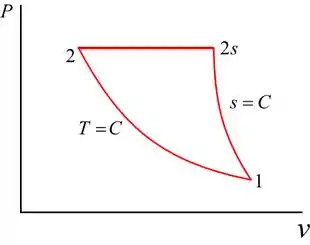
Passo 3
Calculando o trabalho requerido para compressão isotérmica:
Sendo:
Temos:
Integrando:
Substituidos os dados:
Passo 4
Calculando o trabalho requerido compressão isentrópica de 2 a 2s.
Primeiramente calculamos a temperatura de pico:
Sendo:
;
;
;
.
Temos:
Passo 5
Calculando o trabalho requerido:
Sendo:
.
Temos:
Passo 6
Calculando a energia removida durante o resfriamento para o processo.
Considerando que de 2s a 2 seja a pressão constante:
Sendo:
.
Temos: