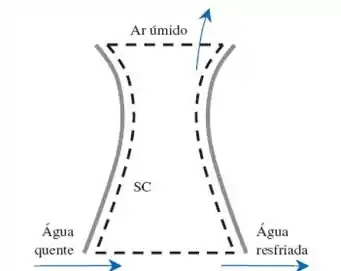
Uma torre de arrefecimento resfria água quente, pulverizando a contra um escoamento forçado de ar seco. Uma parte da água evapora nesse ar e é carregada para a atmosfera fora da torre; a evaporação resfria as gotas de água remanescentes, que são coletadas no tubo de saída da torre (com 150 mm de diâmetro interno). Medições indicam que a vazão de água quente é 31,5 kg/s, e a água fria (21ºC) escoa a uma velocidade média de 1,7 m/s no tubo de saída. A massa específica do ar úmido é 1,06 kg/m3. Determine (a) as vazões mássica (kg/s) e volumétrica (L/min) da água fria, (b) a vazão mássica (kg/s) do ar úmido e (c) a vazão mássica (kg/s) do ar seco.
Sugestão: No Google, digite “density of moist air” ou “massa específica do ar úmido” para obter informações sobre a massa específica do ar úmido e seco!
Passo 1
Vamos lá!!
O que ta acontecendo aqui é, água quente ta entrando e se resfriando, mas uma parte dessa água evapora e é carregado pra fora da torre!
O problema pede diversas vazões mássicas e volumétricas das correntes, para isso vamos utilizar a seguinte fórmula:
E:
O enunciado já da o volume de controle de bandeija pra a gente! Então bora colocar a mão na massa!
Passo 2
A letra (a) pede as vazões mássicas e volumétricas da água fria, para isso temos os seguintes dados:
Podemos calcular a área interna do tubo de saída:
Podemos calcular a vazão volumétrica da água fria:
Mas o problema pede em :
Agora podemos calcular a vazão mássica, sabendo que
Passo 3
Agora a gente vai atrás da vazão mássica do ar úmido!
E como a gente faz isso?!
O problema diz pra a gente que a água quente entra e parte dessa água evapora no ar seco e é carregada para fora da torre. É é justamente a vazão mássica desse carinha que a gente quer!
É a parcela da água que evaporou e se ela evaporou ela não esta na corrente de água fria, concorda?!
Então podemos fazer:
a gente achou no passo anterior e , dado no enunciado:
Passo 4
Por fim, a gente quer a vazão mássica do ar seco.
A gente conhece a vazão mássica do ar úmido, mas a gente pode calcular a umidade relativa da seguinte forma:
Ao procurar no google por “massa específica do ar úmido”, achamos a seguinte relação:
Também achamos:
A massa específica do ar seco pode ser achado na tabela no final do livro:
Na tabela achamos:
Isolando o na equação acima:
Substituindo os valores:
Agora que conhecemos , podemos voltar em:
Isolando e substituindo os valores:
Aweeeee!