Um trocador de calor de tubos geminados, com escoamento em contracorrente, opera com vazões iguais de nas correntes de ar quente e de ar frio. A corrente fria entra a e deve ser aquecida até , utilizando o ar quente disponível a . A pressão média das correntes de ar é e a queda de pressão máxima permissível na linha de ar frio é de . Considere que as paredes dos tubos atuam como aletas, cada uma com uma eficiência de .

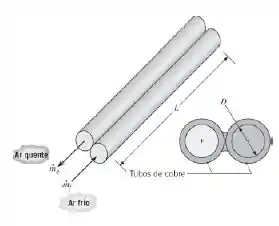
a) Determine o diâmetro e o comprimento dos tubos que satisfazem às exigências de transferência de calor e queda de pressão especificadas.

Como é um trocador de calor balanceado, as taxas de capacidade de ambos os fluxos de ar serão as mesmas:

Desse modo, a razão da capacidade térmica será igual a 1:

Calculando a eficácia do trocador de calor:

Substituindo as temperaturas:

Calculando para o trocador de calor de escoamento contracorrente com taxa de capacidade igual a 1:

Como:

Com:

E

.

Temos:

A expressão para o coeficiente geral de transferência de calor se dá:

Como as condições de fluxo são quase idênticas, os coeficientes de transferência de calor por convecção podem ser aproximadamente iguais, então:

Portanto:

Como:

Então:

Calculando o número de Reynolds:

Substituindo os dados:

Escrevendo uma expressão para o número de Nusselt para o caso de fluxo turbulento totalmente desenvolvido aplicando a equação de Dittus-Botler para aquecimento de ambas as correntes de ar:

Substituindo os dados:

Como:

Então:

A expressão para o fator de atrito para o fluxo turbulento totalmente desenvolvido se dá:

Substituindo :

Já a expressão para a queda de pressão para fluxo totalmente desenvolvido aplicando a equação de Darcy é:

Expandindo:

Sendo:

.

Temos:

Resolvendo as equações dos Passos 4, 5, 6 e 7 simultaneamente utilizando ferramentas matemáticas, obtemos: