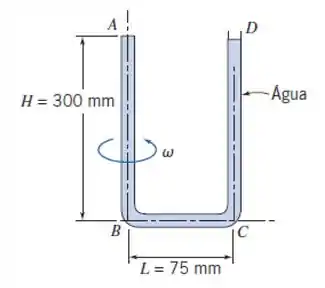
O tubo em U mostrado está cheio com água a T = 20ºC. Ele é vedado em A e aberto para a atmosfera em D. O tubo gira a 1600 rpm em torno do eixo vertical AB. Para as dimensões mostradas, ocorreria cavitação no tubo?
Passo 1
Vamos lá!! O problema trás pra a gente um tubo em girando a no sentido anti-horário e a gente quer saber se ocorreria ou não cavitação, considerando as dimensões do tubo!
Mas o que precisa acontecer pra ocorrer cavitação?!
A pressão no ponto , que é a extremidade fechada, tem que ser maior do que a pressão de vapor da água!
Então queremos saber quem é !!
Vamos usar a equação básica:
Como o tubo esta girando, vamos usar as coordenadas cilindricas, vamos ver um esqueminha de como vai ficar isso:
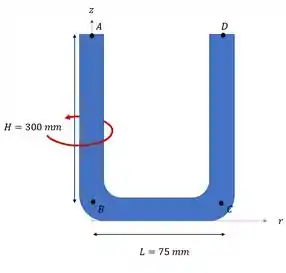
Agora vamos substituir a equação a cima para e para !
Em podemos cancelar a a gravidade, logo:
A aceleração em é centrípeda, e anti-horária, então:
Substituindo:
Agora para , onde a gente só tem a aceleração da gravidade:
Passo 2
A gente escreveu as equações, mas precisamos tirar essas derivadas e para isso só integrando!
Vamos integrar entre pontos, sempre que a gente puder considerar um dos eixos constante!
Entre os pontos e , é constante, então podemos escrever:
Jogando o para a direita, podemos integrar:
Integrando:
Entre e , também é constante, esta na mesma altura que e por sua vez na mesma altura que , então podemos reaproveitar a integral que calculamos para e :
Agora entre e , é constante, então podemos usar:
Podemos fazer:
Integrando:
Passo 3
Beleza, temos todas as equações! Mas agora pra atacar elas a gente precisa pensar em que ponto temos informações, é daí que vamos começar!
No ponto temos o tubo aberto, então podemos dizer que :
Pegando a equação:
Podemos tirar substituir , isolando ficamos com:
Agora conhecemos e onde mais aparece?!
Podemos substituir, certo?
Agora que conhecemos , podemos finalmente achar :
Isolando e substituindo :
Opaaa, da pra cancelar esse ai:
Agora a gente tem uma equação com variáveis que conhecemos!!
Passo 4
Agora a gente só precisa calcular e compara com a pressão de vapor da água:
Considerando que esse exprerimento acontece no nível do mar:
O fluido é agua, então:
Relembrando os dados do problema:
Substituindo:
Agora basta saber se essa pressão é maior que a da água a :
logo, não haverá cavitação!
Resposta
logo, não haverá cavitação.