Para o regador giratório do Exemplo 4.14, que valor de produzirá a máxima velocidade de rotação? Que ângulo fornecerá a máxima área de cobertura do regador? Desenhe um diagrama de velocidades (usando um sistema de coordenadas r, θ, z) para indicar a velocidade absoluta do jato de água deixando o bocal. O que governa a velocidade de rotação do regador no regime permanente? A velocidade de rotação do regador afeta a área coberta pelos jatos de água? Como você estimaria essa área? Para α fixo, o que pode ser feito para aumentar ou diminuir a área coberta pelos jatos de água?
Passo 1
Pra começar com o pé direito, vamos desenhar um esqueminha do que ta acontecendo!
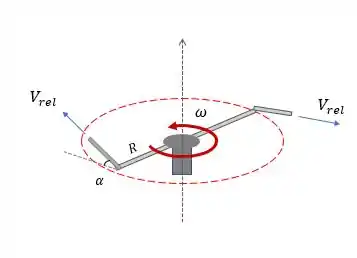
No exemplo a gente pode tirar a seguinte relação:
Essa questão pede várias coisinhas! Então em cada passo a gente vai discutir o que a gente quer e como fazemos pra encontrar! Belezinha?
Passo 2
Primeiro a gente quer que a velocidade de rotação seja a maior possível e a gente quer saber qual deve ser o valor de pra isso!
Usando a relação que vimos a cima:
Isolando :
Bem,temos , o valor máximo de , para que isso aconteça !
Substituindo:
Observando essa euquação a gente pode responder mais uma pargunda, que é o que governa a velocidade de rotação! Ou seja, quem manda na velocidade de rotação !
Teminamos de calcular e vimos o quanto isso depende do ângulo ! Além do também tem uma variável muito importante que é o torque !
Passo 3
Agora o que a gente quer saber é, que ângulo fornecerá a máxima área de cobertura do regador!
A cobertura máxima do regador é o alcance máximo dele, ou seja, o mais longe que ele pode alcançar, ignorando o arrasto aerodinâmico do fluxo.
Desenhando o diagrama de velocidades:
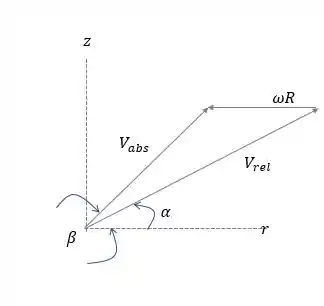
Aqui o que a gente tem é nada mais nada menos do que o lançamento oblíquo da água, certo?!!
Para um lançamento oblíquo o alcance é máximo, ou seja, é máximo quando !
Passo 4
Agora vamos conversar sobre a velocidade de rotação e a área coberta pelos jatos de água!!
Olhando a figura do irrigador a gente vê que a rotação é anti-horária, é como se ele puxasse o jato de água pra cima!
Quando o irrigador ta parado a gente tem e , a medida que o irrigador começa a girar começa a aumentar, porque a esta “puxando” o jato de água pra cima e aumentando o ângulo com .
Agora imagina que você esta com uma dessas pistolas de água na mão, você concorda que quando mais vc levanta o braço, mais perto o jato de água vai cair de você?! Inclusive se você levantar totalmente os braços, o jato de água vai cair em cima de você!
Se eu diminuo o alcance máximo, logo eu diminuo a área de irrigação!
Logo, se eu aumento eu diminuo a área irrigada!
Passo 5
Agora, como a gente poderia calcular a área irrigada?!
Se eu to com o irrigador parado eu irrigo duas linhas, certo?! Logo se eu começo a rodar eu irrigo uma área redonda com raio igual ao alcance do irrigador, logo:
Onde é o alcance do irrigador!
Resposta
Ei, a resposta está no passo a passo :)