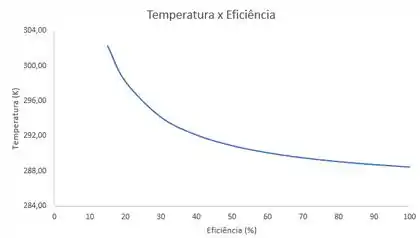
Com o uso, a eficiência do compressor do Problema 12.17 diminui. Para qual eficiência a potência requerida, para atingir 8,0 MPa (manométrica), excederá 30 MW? Trace o gráfico da potência requerida e da temperatura de saída do gás como funções da eficiência.
Passo 1
Vamos lá!! No problema temos um compressor, o fluido de trabalho é metano e as informações sobres as correntes de entrada e saída são:
Temos também os seguintes dados tabelados:
Mas afinal, o que a gente quer?!
Na questão anterior a gente tinha a eficiência e queriamos a potência! Mas agora a eficiência não é a mesma e como a eficiência diminuiu eu vou precisar usar uma potência maior pra chegar no mesmo resultado de pressão!
A eficiência é dada por:
Se a corrente de entrada é igual pros dois casos, então quem vai mudar é , temos que achar ele para achar a nova eficiência!
Passo 2
Temos essa expressão aqui, obedecendo a primeira lei da termodinâmica:
Mas:
Então:
Para calcular a vazão mássica:
Ficamos com:
Substituindo os valores:
Para achar :
Isolando :
Substituindo:
Passo 3
Temos todos os dados menos a temperatura de saída, o problema é que não é nada simples isolar , então vamos colocar cada pra um lado e resolver usando o Solver do excel!
Vai ficar assim:

Então temos:
Passo 4
Voltando na equação de eficiência:
é para o caso isentrópico, esse valor foi achado no problema :
Substituindo os valores:
Calculando:
Passo 5
Agora temos dois gráficos pra traçar!
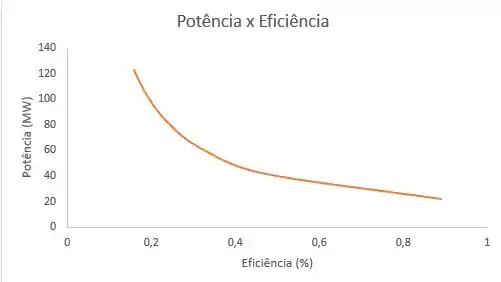
O primeiro é da potência requerida como função da eficiência:
Usando:
E:
Temos:
Passo 6
Agora o gráfico temperatura em função da eficiência:
Trace o gráfico da potência requerida e da temperatura de saída do gás como funções da eficiência.
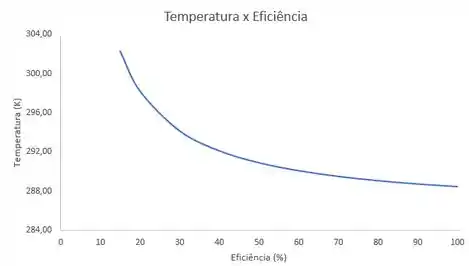
Resposta
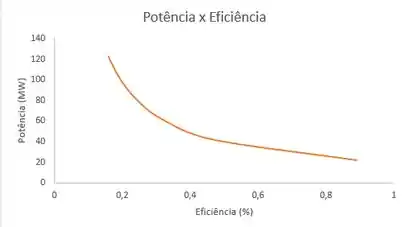
e