Verifique que xp = −asen(ωt), yp = acos(ωt) é a equação para as trajetórias de partículas para o campo de escoamento do Problema 2.12. Determine a frequência de movimento ω como uma função da amplitude de movimento, a, e K. Verifique que xp = −asen(ωt), yp = acos(ωt) é também a equação para as trajetórias de partículas para o campo de escoamento do Problema 2.11, exceto que ω agora é uma função de M. Trace trajetórias típicas para ambos os campos de escoamento e discuta a diferença.
Passo 1
Pra quem não pode ver uma função trigonométrica que já fica desesperado! Calma!
O exercício pede várias coisas e a medida que a gente for caminhando a gente vai discutir como chegamos nelas!
Mas primeiro vamos organizar primeiro as informações do enunciado, começando pelas equações do campo de escoamento:
Ai o problema fala do campo de escoamento do problema , que é:
Bora colocar a mão na massa??!!
Passo 2
Vamos começar substituindo:
A gente ta vendo ali um , um , isso nos lembra aquela identidade trigonométrica:
Certo?!! Então vamos manipular a expressão pra chegar lá:
Tem um sinal negativo alí na frente do que ta atrapalhando a gente, podemos fazer:
E ficamos com:
Agora é só isolar o :
Ficamos com:
Agora vamos fazer o mesmo com :
Substituindo:
Fazendo as mesmas manipulações que fizemos com :
Passo 3
Agora temos:
E:
Considerando a equação do livro, temos:
Vamos derivar e em relação a , considerando e constantes:
Agora a gente compara e com as equações que a gente chegou no final do passo 2:
Dessa comparação tiramos:
Isolando o :
Com isso a gente acaba a primeira parte do exercício, que pede pra verificar que e são equações para as tragetórias das particulas para o campo de escoamento do problema .
Sim, a afirmação esta correta, desde que:
Passo 4
Agora a gente vai determinar a frequência de movimento ω como uma função da amplitude de movimento, e .
Então vamos lá!! Para plotar isso no Excel, vamos calcular e para variando de a , com ω dado pela fórmula acima!
Ficamos com:
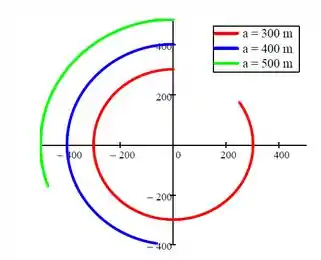
Observe que as partículas externas viajam muito mais devagar!
Passo 5
Agora a gente vai verificar que e também são equações para as tragetórias das partículas para o campo de escoamento o problema .
Ou seja, vamos fazer a mesma coisa que fizemos para o problema !
Do problema temos:
Relembrando quem é e :
Substituindo:
Lá em cima derivamos e em relação a , vamos relembrar:
Agora comparando:
Pela comparação podemos tirar:
Isolando o :
Achamos a condição para a afirmação ser verdadeira!
Passo 6
Por fim a gente tem a tragetória típica para este campo de escoamento:
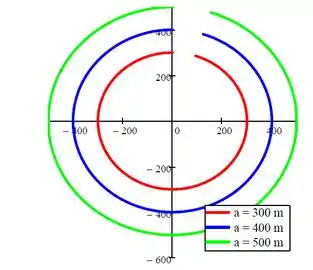
Resposta
Ei, a resposta está no passo a passo :)