Em 1816, Robert Stirling, um clérigo escocês, patenteou o motor de Stirling, que teve uma variedade de aplicações desde então, incluindo a da potência solar discutida neste livro. O combustível é queimado externamente para aquecer um dos dois cilindros do motor. Uma quantidade fixa de gás inerte se move ciclicamente entre os cilindros, expandindo-se no cilindro quente e se contraindo no frio. A Figura P18.47 representa um modelo para esse ciclo termodinâmico. Considere n mols de um gás ideal monoatômico passando pelo ciclo uma vez, consistindo em dois processos isotérmicos a temperaturas 3Ti e Ti e dois processos de volume constante. Vamos encontrar a eficiência desse motor. (a) Encontre a energia transferida por calor para o gás durante o processo isovolumétrico AB. (b) Encontre a energia transferida por calor para o gás durante o processo isotérmico BC. (c) Encontre a energia transferida por calor para o gás durante o processo isovolumétrico CD. (d) Encontre a energia transferida por calor para o gás durante o processo isotérmico DA. (e) Identifique quais dos resultados das partes (a) a (d) são positivos e avalie a entrada de energia no motor por calor. (f) A partir da Primeira Lei da Termodinâmica, encontre o trabalho realizado pelo motor. (g) A partir dos resultados das partes (e) e (f), avalie a eficiência do motor. É mais fácil manufaturar um motor de Stirling que um de combustão interna ou uma turbina. Ele funciona com lixo queimado. E pode funcionar com energia transferida pela luz do sol e não produzir material de escape. Motores de Stirling não são usados em automóveis atualmente por causa do longo tempo de partida e resposta pobre de aceleração.
Passo 1
Fala galera, beleza? Bora resolver o nosso exercício? Vamos lá.
O processo acontece numa região com temperatura constante, ou seja, acaba sendo um processo isotérmico.
Além disso, ele também se trata de um processo com volume constante, ou seja, isovolumétrico.
Vamos dar uma olhada na figura para entender melhor o que está acontecendo?
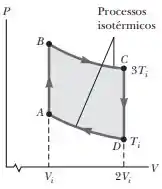
Show, vamos começar pelo processo AB. Reparem que nele, o volume se mantém constante, ou seja, a variação do volume vai ser igual a zero. E por que isso vai ser importante? Se liga
Como :
Beleza, algo também que precisamos saber aqui é usar a equação de energia transferida da primeira lei da termodinâmica:
Show, e agora? Se liga
Pelo enunciado, , então:
Passo 2
Vamos fazer o mesmo para a letra (b), mas agora vamos pegar o trajeto BC:
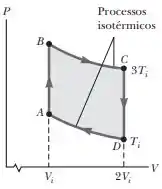
Como se trata de um sistema isotérmico, a temperatura do gás é constante e ai com isso a variação da sua energia interna é igual a zero
Show, com isso a gente consegue calcular o trabalho
Beleza, agora, se a gente usar a mesma equação do Passo 1, vamos conseguir achar o valor da transferência de energia:
Passo 3
Show, agora vamos para a letra (c), vamos pegar o trajeto CD:
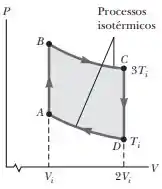
O cenário aqui é igual ao do Passo 1 (trajeto AB), então vamos usar as mesmas fórmulas e valores para alguns casos. Como se trata de um sistema isotérmico, a temperatura do gás é constante e aí com isso a variação da sua energia interna é igual a zero
Para calcularmos a energia:
Pelo enunciado, e , então:
Passo 4
Show, agora vamos para a letra (d), vamos pegar o trajeto DA:
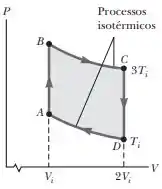
O cenário aqui é igual ao do Passo 2 (trajeto BC), então vamos usar as mesmas fórmulas e valores para alguns casos. Como o volume é constante, já podemos então dizer que:
Para calcularmos o trabalho:
Beleza, agora, se a gente usar a mesma equação do Passo 1, vamos conseguir achar o valor da transferência de energia:
Passo 5
Agora vamos calcular o trabalho total feito pelos processos:
Passo 6
Por último, vamos calcular a eficiência. Para isso, vamos usar:
Reparem que a gente pode simplificar bastante:
Resposta
Ei, a resposta está no passo a passo :)