Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 44.Problemas adicionais - Ex. 49

49. A figura 44.13 mostra parte do arranjo experimental que levou a descoberta dos antipróton na década de 1950 . Os pesquisadores fizeram um feixe de prótons de 6,2   G e V , produzido em um acelerador de partículas, colidir com núcleos atômicos em um alvo de cobre. De acordo com as previsões teóricas da época, as colisões com os prótons e nêutrons dos núcleos de cobre deveriam produzir antiprótons através das reações:

p + p → p + p + p + p

p + n → p + n + p + p

Entretanto, mesmo que estas reações ocorressem, seriam raras em comparação com as reações:

p + p → p + p + π + + π -

e

p + n → p + n + π + + π -

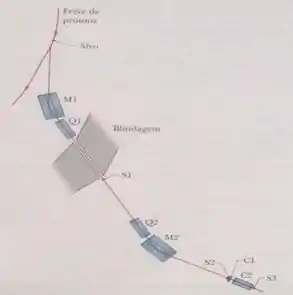
Assim, esperava-se que a maioria das partículas produzidas pelas colisões entre os prótons de 6,2   G e V e o alvo de cobre fossem píons. Para provar que os antiprótons existiam e eram produzidos em pequeno número nas colisões, os pesquisadores fizeram as partículas que deixassem o alvo passar por uma série de campos magnéticos e detectores, como mostra a Fig. 44-13. O primeiro campo magnético (MI) encurvava a trajetória das partículas de tal forma que para chegar ao segundo campo magnético (QI), as partículas tinham que ter carga negativa e um Momento de 1,19   G e V / c . Isso excluía todas as partículas, exceto os antiprótons ( p - ) e. os píons negativos ( π - ) . Ql era um tipo especial de ~ampo magnéttc? (campo quadrupolar) usado para focalizar as partículas em um feixe estreito, permitindo que atravessassem um furo na blindagem para chegar ao cintilômetro SI. A passagem pelo cintilômetro de uma partícula carregada produzia um sinal que indicava a chegada de um píon negativo de 1,19   G e V / c ou (possivelmente) de um antipróton de 1,19   G e V / c .

Depois de ser focalizado novamente pelo campo magnético Q2, o feixe era dirigido pelo campo magnético M2 para um segundo cintilômetro, S2, seguido por dois contadores de Cerenkov, CI e C2, que emitiam un1 sinal apenas quando atravessados por uma partícula cuja velocidade estava dentro de um certo intervalo. No experimento, uma partícula com uma velocidade maior que 0,79 c fazia disparar o contador C1, enquanto uma partícula com uma velocidade entre 0,75 c e 0,78 c fazia disparar o contador C2.

Havia, portanto, duas formas de distinguir os antiprótons (mais raros) do píons negativos (mais abundantes). Ambas se baseavam no fato de que a velocidade de um p - de 1,19   G e V / c e a de um π -   de 1,19   G e V / c são diferentes: (1) de acordo com os cálculos, um p - dispararia um dos contadores de Cerenkov e um π - dispararia o outro; (2) o intervalo de tempo ∆ t entre os sinais produzidos pelos cintilômetros S1 e S2, que estavam separados por uma distância de 12   m , seria diferente para as duas partículas. Assim, se o contador de Cerenkov correto fosse disparado e o intervalo de tempo ∆ t tivesse o valor correto, o experimento provaria a existência de antiprótons.

Qual é a velocidade (a) de um antipróton com um momento de 1,19   G e V / c ; (b) de um píon negativo com o mesmo momento? (A velocidade de um antipróton ao passar pelos detectores de Cerenkov seria na verdade ligeiramente menor que o valor calculado, já que o antipróton perderia um pouco de energia no interior dos detectores.) Qual dos detectores seria disparado (c) por um antipróton; (d) por um píon negativo? Qual seria o intervalo de tempo ∆ t (e) para um antipróton e (f) para um píon negativo?

Passo 1

a) Bom! Para resolver essa letra vamos usar a seguinte equação abaixo que já aprendemos no capítulo 37 , para expressar a relação relativística entre velocidade e momento:

p = γ m v = m v 1 - ( v / c ) 2

Agora, vamos trabalhar um pouco mais em cima dessa expressão, afinal é a velocidade v que queremos obter.

Por isso, bora tratar de deixar tudo em função de v :

p = m v 1 - ( v / c ) 2

p 2 = ( m v ) 2 1 - ( v / c ) 2

p 2 - p 2 v 2 c 2 = m 2 v 2

c 2 p 2 - p 2 v 2 = m 2 v 2 c 2

p 2 v 2 + m 2 v 2 c 2 = c 2 p 2

v 2 p 2 + m 2 c 2 = c 2 p 2

v = c 2 p 2 p 2 + m 2 c 2 = c p 2 p 2 + m 2 c 2

Não tá legal essa expressão né, não? O que acha de multiplicarmos em cima e em baixo na raiz, por c 2 :

v = c p 2   c 2 p 2   c 2 + m 2 c 4

Agora, bora dividir tudo por p 2 c 2 :

v = c p 2 c 2 p 2 c 2 + m 2 c 4

v = c p 2 c 2 p 2 c 2 p 2 c 2 p 2 c 2 + m 2 c 4 p 2 c 2

v = c 1 1 + m 2 c 4 p 2 c 2

v = c 1 1 + m c 2 p c 2

Pronto! Agora ficou bem mais fácil! Sabe por quê!? Porque para um antipróton; já temos os valores tabelados de m c 2 e p c :

p c = 1190   M e V

m c 2 = 938,3   M e V

Com isso, façamos o cálculo:

v = c 1 1 + 938,3   M e V 1190   M e V 2

v = 0,785 c

Passo 2

b) E para achar o valor da velocidade, no caso de um píon negativo; usemos a mesma expressão do P a s s o   1 , sabendo que desta vez no caso do píon:

p c = 1190   M e V

m c 2 = 193,6   M e V

v = c 1 1 + 193,6   M e V 1190   M e V 2

v = 0,993 c

Passo 3

c) Bom! A velocidade dos antiprótons está entre 0,75 e 0,79 . Logo, como obtivemos um valor nesse faixa, temos que o antipróton faria disparar o detector C2.

Passo 4

d) A velocidade dos píons negativos é maior que 0,79 . Como obtivemos um valor maior que isso, temos que um píon negativo faria disparar o detector C1.

Passo 5

e) E para achar o intervalo de tempo decorrido, bastar usar a relação entre distância percorrida, no caso 12   m , e a velocidade:

d = v ∆ t

∆ t = d v

Façamos então, o cálculo pro antipróton:

∆ t = 12   m 0,785 ⋅ 2,998 ⋅ 10 8   m / s

∆ t ≅ 51   n s

Passo 6

f) Depois, façamos o cálculo pro píon:

d = v ∆ t

∆ t = d v

∆ t = 12   m 0,993 ⋅ 2,998 ⋅ 10 8   m / s

∆ t ≅ 40   n s

Resposta

a) v = 0,785 c

b) v = 0,993 c

c) O   a n t i p r ó t o n   f a r i a   d i s p a r a r   o   d e t e c t o r   C 2 .

d) O   p í o n   n e g a t i v o   f a r i a   d i s p a r a r   o   d e t e c t o r   C 1 .

e) ∆ t ≅ 51   n s  

f) ∆ t ≅ 40   n s  

Ver Outros Exercícios desse livro