Desvio cosmológico para o vermelho. A expansão do universo é representada frequentemente por um desenho como o da Fig. . Na figura, estamos situados no ponto VL (as iniciais de Via Láctea, a nossa galáxia), na origem de um eixo que se afasta de nós em uma direção qualquer. Outras galáxias, muito distantes da nossa, também estão representadas. As setas associadas a essas galáxias mostram a velocidade de cada uma, de acordo com o desvio para o vermelho da luz que recebemos. Segundo a lei de Hubble, a velocidade de cada galáxia é proporcional à distância que a separa de nós. Desenhos como esse podem causar uma impressão errônea, porque parecem mostrar que os desvios para o vermelho se devem ao movimento das galáxias em relação à Terra, enquanto se deslocam em um espaço estático (estacionário), e que estamos no centro de todo esse movimento.

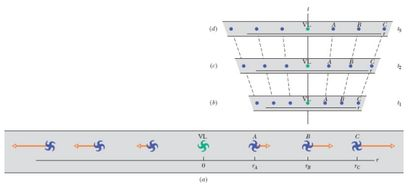
Na verdade, a expansão do universo e o aumento da distância entre as galáxias não se devem ao movimento divergente das galáxias em um espaço preexistente, mas à expansão do próprio espaço. O espaço não é estático, e sim dinâmico. As Figs. mostram uma forma diferente de representar o universo e sua expansão. Cada parte da figura constitui uma seção unidimensional do universo (ao longo do eixo ); as outras duas dimensões espaciais do universo não são mostradas. Cada uma das três partes da figura mostra a Via Láctea e seis outras galáxias (representadas por pontos); as seções estão situadas em diferentes posições ao longo do eixo dos tempos, com . Na seção , a mais antiga, a Via Láctea e as seis outras galáxias estão mais próximas entre si. Com a passagem do tempo, o universo se expande, o que faz aumentar a distância entre as galáxias. Observe que as figuras foram traçadas do ponto de vista da Via Láctea e por isso as outras galáxias parecem se afastar da Via Láctea por causa da expansão. Na verdade, a Via Láctea não ocupa uma posição especial; as galáxias também pareceriam se afastar de qualquer outro ponto escolhido como referência. As Figs. mostram apenas a Via Láctea e uma das outras galáxias, a galáxia , em dois instantes de tempo diferentes durante a expansão. Na Fig. , a galáxia se encontra a uma distância da Via Láctea e está emitindo uma onda luminosa de comprimento de onda . Na , após um intervalo de tempo , a onda está sendo detectada na Terra. Vamos chamar de a taxa de expansão do universo por unidade de tempo e supor que essa taxa se mantém constante durante o intervalo de tempo . Nesse caso, durante o intervalo , todas as dimensões espaciais sofrem uma expansão de ; assim, a distância aumenta de . A onda luminosa das Figs. e se propaga com velocidade da galáxia até a Terra. Mostre que

O comprimento de onda detectado, , é maior que , o comprimento de onda emitido, porque o espaço se expandiu durante o intervalo de tempo . Esse aumento do comprimento de onda é chamado de desvio cosmológico para o vermelho; não se trata de um efeito Doppler. Mostre que a variação do comprimento de onda é dada por

Calcule a expansão binomial (veja o Apêndice ) do lado direito da equação. Qual é o valor da razão se for conservado apenas o primeiro termo da expansão?

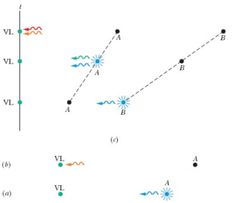
Por outro lado, se usarmos o modelo da Fig. e supusermos que o desvio para o vermelho se deve ao efeito Doppler, teremos, de acordo com a Eq. ,

em que é a velocidade radial da galáxia em relação à Terra. Depois de usar a lei de Hubble para determinar a velocidade da galáxia , compare o valor da razão , obtido usando esse modelo, com o resultado do item e calcule o valor de em termos da constante de Hubble. Essa análise mostra que os dois modelos usados para explicar o desvio para o vermelho das galáxias distantes levam aos mesmos resultados. Suponha que a luz proveniente da galáxia apresente um desvio para o vermelho e que a taxa de expansão do universo tenha se mantido constante, com o valor dado neste capítulo, desde que a luz foi emitida pela galáxia. Use o resultado do item para calcular qual era a distância entre a galáxia e a Terra na época em que a luz foi emitida. Determine há quanto tempo a luz foi emitida pela galáxia usando o resultado do item e supondo que o desvio para o vermelho se deva ao efeito Doppler. [Sugestão: No caso do item , o tempo é dado pela distância no instante da emissão dividida pela velocidade da luz, já que, como estamos imaginando que o desvio para o vermelho se deve ao efeito Doppler, a distância não varia durante o tempo que a luz leva para chegar à Terra. Nesse caso, os resultados dos dois modelos são diferentes.] Qual é a distância entre a galáxia e a Terra no instante em que a luz é detectada? (Estamos supondo que a galáxia ainda existe; se ela deixasse de existir, os humanos só tomariam conhecimento do fato no instante em que a última luz emitida pela galáxia chegasse à Terra.) Suponha que a luz proveniente da galáxia (Fig. ) apresente um desvio para o vermelho . (j) Use o resultado do item para determinar a distância entre a galáxia e a Terra no instante em que a luz foi emitida. Use o resultado do item para determinar há quanto tempo a luz foi emitida pela galáxia . Quando a luz que detectamos da galáxia foi emitida, qual era a distância entre a galáxia e a galáxia ?

Vamos começar com o item .

Do enunciado sabemos que a luz emitida pela galáxia tem uma velocidade igual a e depois de um intervalo é foi detectada na Terra, então ele percorreu uma distância de .

O enunciado também diz que nesse intervalo de tempo o espaço entre a Terra e galáxia sofreu uma expansão de , então a distância inicial entre a Terra e a galáxia sofreu um acréscimo igual a essa expansão, assim a nos distância é dada por:

Então se a luz percorreu uma distância c até a Terra e a distância entre a Terra e a galáxia é , então uma coisa é igual a outra, logo:

Agora isolando , temos:

Chegamos onde o item queria.

Agora vamos para o item .

O enunciado diz que o comprimento de onda detectado na Terra é maior que o emitido pela galáxia esse aumento no comprimento de onda é por conta da expansão do espaço, e como a taxa de expansão do espaço é dada por , temos que:

Agora vamos analisar a razão , temos:

Substituindo a expressão de , temos:

Então temos que:

Usando a expressão para que encontramos em já que é o tempo que a luza demorou para chegar na Terra, temos:

Agora vamos para o item .

Agora temos que usar a expansão binomial para expandir o termo da direita da equação que encontramos no item , a expansão é da seguinte forma:

Par isso temos que rescrever o termo da direita da equação do item de uma forma parecida com o termo da expansão, temos:

Agora podemos expandir o termo , assim teremos que:

Então temos que:

Com isso temos que:

Agora vamos para o item .

Aqui ele quer o valor da razão quando só é levado em conta o primeiro termo da expansão que fizemos antes, assim:

Agora vamos para o item .

A lei de Hubble é dada por:

Onde é a constante de Hubble e é a distância entre a as galáxias considerando o modelo da figura do enunciado, então usando a relação o item nos deu, temos:

Comparando com o que achamos no item , teremos que:

Temos o que ele queria!

Agora vamos para o item .

Para calcularmos a distância entre a galáxia e a Terra na época em que a luz foi emitida que o item quer, vamos usar a expressão que chegamos no item , temos:

Agora temos que isolar já que essa é a distância inicial entre a Terra e a galáxia, temos:

Então temos que:

Do enunciado temos que e do livro temos que , então temos que:

Essa era a distância entre a Terra e a galáxia, quando a luz foi emitida.

Agora vamos para o item .

Agora queremos a quanto tempo a luz foi emitida pela galáxia usando a expressão do item , temos:

A distância é a distância entre a Terra e a galáxia quando a luz foi emitida, isso a gente já tem do item anterior, assim:

Mas vamos encontrar esse tempo em segundos, assim vamos usar que em temos , assim:

Agora vamos para o item .

O tempo considerando o desvio para o vermelho como sendo causado pelo efeito Doppler é dado da seguinte forma (como o enunciado fala):

Usando que , temos que:

Agora vamos para o item .

Para encontramos a distância entre a Terra e galáxia para esse caso, basta usarmos que:

Considerando o com melhor valor que é o que consideramos a expansão do espaço, temos:

Como já vimos, em temos então:

Vamos para mais um item, a letra .

Nesse item, também vamos usar o resultado do item para calcular a distância entre a galáxia e a Terra, para o caso de , fazendo a mesma manipulação que fizemos em , temos o seguinte:

Do livro temos que , então temos que:

Essa era a distância entre a Terra e a galáxia , quando a luz foi emitida.

Vamos para mais um item, a letra , uma hora acaba kkkk.

Agora queremos a quanto tempo a luz foi emitida pela galáxia usando a expressão do item , temos:

A distância é a distância entre a Terra e a galáxia quando a luz foi emitida, isso a gente já tem do item anterior, assim:

Mas vamos encontrar esse tempo em segundos, assim vamos usar que em temos , logo:

Finalmente vamos para o último item!! Letra .

A distância entre e quando detectamos a luz de é dada pela diferença entre as distâncias de até a Terra e de até a Terra, assim:

Sabemos também que o espaço se expande, então a distância entre essas galáxias quando a detectamos o sinal de pode ser dada por:

A lógica dessa situação é bem parecida com a do item , assim:

Isolando , temos:

Agora temos que tomar cuidado no produto pois ele precisa ser adimensional para ser somado a , temos que:

Agora usando o fato de que em temos , teremos:

Agora substituindo tudo o que temos, ficamos:

Passando para , temos:

Finalmente conseguimos terminar essa questão!! Deu trabalho, mas conseguimos detonar com ela!