Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 43.Problemas adicionais - Ex. 56

56. A expressão da distribuição de velocidades de Maxwell das moléculas de um gás é dada no Capítulo 19. (a) Mostre que a energia mais provável é dada por:

K P = 1 2 k T

Mostre que este resultado está correto para curva n ( K ) da figura 43.10 que foi traçada para T = 1,5 ⋅ 10 7   K . (b) Mostre que a velocidade mais provável é dada por:

v p = 2 k T m

Calcule o valor de v p para o caso de prótons a uma temperatura T = 1,5 ⋅ 10 7   K . (c) Mostre que a energia correspondente a velocidade mais provável (que não é a mesma coisa que energia mais provável) é dada por:

K v , p = k T

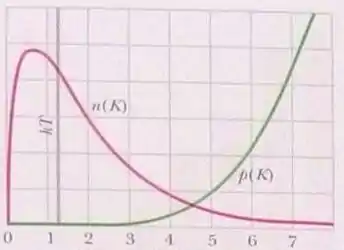
Assinale esse ponto na curva de n ( k ) da figura 43 - 10

Passo 1

a) Bom! Vamos usar a expressão de n ( K ) do problema 34 desse capítulo em nossa análise; afinal é uma expressão mais conveniente. De acordo com ela, a concentração de prótons por unidade de energia é dada por:

n K = 1,13 n ⋅ K 1 / 2 k T 3 / 2 e - K / k T

E como queremos determinar a energia mais provável, precisamos derivar n ( K ) em relação a K e igualar o resultado a zero. Vamos lá!

d d K n K = d d K 1,13 n ⋅ K 1 / 2   k T 3 / 2 e - K k T = 0

1,13 n k T 3 / 2 d d K K 1 / 2   e - K k T = 0

1,13 n k T 3 / 2 1 2 K 1 / 2 - K 1 / 2 k T e - K k T = 0

Agora, que já derivamos a nossa expressão, vamos resolver essa equação e ver qual valor de K

iremos pegar:

1,13 n k T 3 / 2 1 2 K 1 / 2 - K 1 / 2 k T e - K k T = 0

1 2 K 1 / 2 - K 1 / 2 k T = 0

k T - 2 K 2 k T K 1 / 2 = 0

k T - 2 K = 0

K = k T 2

Esse é o valor de K que queremos usar, também chamado de K p . E como sabemos o valor da temperatura que nos é fornecida e que a constante k vale 8,62 ⋅ 10 - 5   e V / K ; façamos o cálculo:

K = K p = ( 8,62 ⋅ 10 - 5   e V / K ) ( 1,5 ⋅ 10 7   K ) 2

K p = 646,5   e V ≅ 0,65   k e V

E esse resultado está perfeitamente condizente com o observado na figura 43 - 10 , pela curva em verde:

Passo 2

b) No estudo dos gases, temos que a velocidade mais provável de um gás é dada pela seguinte fórmula:

v p = 2 R T M

Onde M é a massa molar do gás. Como a massa molar está relacionada à massa das moléculas do gás através da equação   M = m N A , na qual N A é o número de Avogadro, e a constante dos gases perfeitos R está relacionada à constante de Boltzmann k através da equação escrita na forma R = k N A , temos que v p pode ser reescrita como:

v p = 2 R T M = 2 k N A T m N A

v p = 2 k T m

Sabendo o valor da temperatura que já nos foi fornecido, da constante de Boltzmann k igual a 1,38 ⋅ 10 - 23   k g ⋅ m 2 ⋅ s - 2 ⋅ K - 1   e que a massa de um próton é estimada em 1,67 ⋅ 10 - 27   k g , façamos as contas para ver se o resultado é satisfatório:

v p = 2 ( 1,38 ⋅ 10 - 23   k g ⋅ m 2 ⋅ s - 2 ⋅ K - 1 ) ( 1,5 ⋅ 10 7   K ) 1,67 ⋅ 10 - 27   k g

v p ≅ 5 ⋅ 10 5   m / s

Passo 3

c) E para esse item, como estamos averiguando o quanto valeria a energia para a situação em que a velocidade é mais provável, basta calcular a energia cinética para esse caso:

K v p = 1 2 m v p 2

E sabemos que:

v p = 2 k T m

O que nos faz ficar com:

K v p = 1 2 m 2 k T m 2

K v p = 1 2 m 2 k T m

K v p = k T

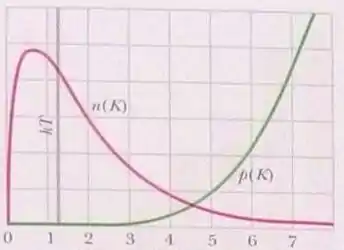
Esse é o dobro da energia que obtivemos na letra (a); portanto igual a aproximadamente 1,3   k e V . E ao olhar a figura 43 - 10 , podemos perceber que a curva que mais se aproxima é a reta na vertical que está em lilás:

Resposta

a) K p ≅ 0,65   k e V =   k T / 2

b) v p ≅ 5 ⋅ 10 5   m / s  

c) K v p ≅ 1,30   k e V = k T  

Ver Outros Exercícios desse livro