Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 5.Problemas - Ex. 87
Passo 1
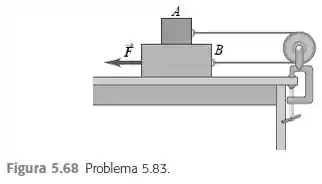
Para identificar a força que vai equilibrar tudo isso aí, vamos fazer diagramas de força para cada corpo. Começando pelo bloco Nele estão agindo a força normal e o peso , ambas possuem mesmo módulos e sentido contrário (NÃO FORMAM PAR AÇÃO REAÇÃO!). E também temos na horizontal a força tensora e para contrabalançar temos a força de atrito que é entre os blocos. O diagrama fica assim:
Devemos lembrar que o sistema de movimenta com VELOCIDADE CONSTANTE! Então todas as forças estão OBRIGATORIAMENTE em equilíbrio:
Passo 2
Beleza! Agora vamos olhar apenas para o bloco ! No bloco temos várias forças agindo. Primeiro vamos às forças que já conhecemos: a força peso para baixo e a normal (reação do contato do bloco na superfície) para cima. Temos também a força (que o problema pede) para a esquerda e a força de tensão para a direita.
Temos também a força de atrito do bloco com o chão e agora uma novidade: temos a força de atrito entre os blocos . Tanto quanto são contrárias à força . Outra força existente aqui e que é muito importante é a força normal e ela aponta para baixo! Sim! Essa é a força com que o bloco empurra o bloco pra baixo!
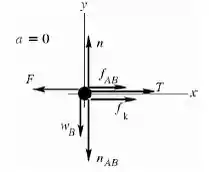
Juntando todas essas informações, o diagrama de forças do bloco é:
Precisamos lembrar que o sistema todo está em equilíbrio, então a soma de todas as forças numa mesma direção é zero!
Na direção vertical nós temos:
E na direção horizontal temos: