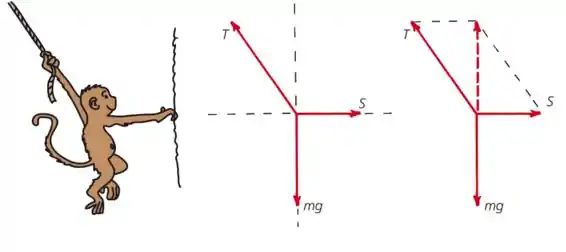
5.69. Com referência ao macaco Mo da Figura 5.26. Se a corda formar um ângulo de 45o com a vertical, como se compararão os módulos dos vetores S e mg
Passo 1
Vamos lá, dá uma olhadinha na figura 5.26 antes de continuar aqui.
Então a gente tem a seguinte configuração de vetores:
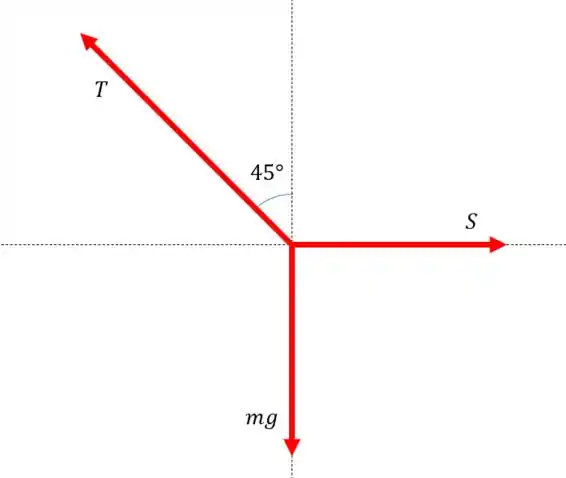
Aqui o segredo é reparar que a força resultante agindo no macaco Mo é nula. Parece que ele está se balançando, mas no próprio livro diz que o macaco está em repouso.
Passo 2
Se a força total agindo no Mo é zero, então a soma dos vetores tem que ser zero também. Olha só, a tensão na corda está em 45° em relação ao eixo vertical, e a gente sabe que a soma de todos os vetores tem que ser zero. Então a resultante de e tem que se cancelar com .
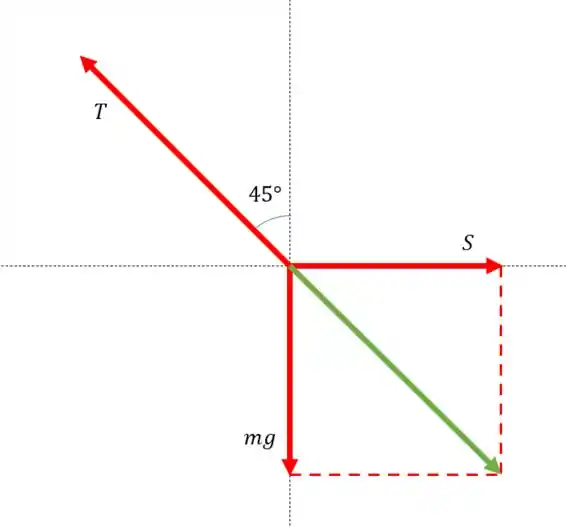
O vetor verde tem que ser igual e oposto ao vetor , isso só pode acontecer se os dois estiverem na mesma direção, então, o vetor verde tem que estar a com a vertical também.
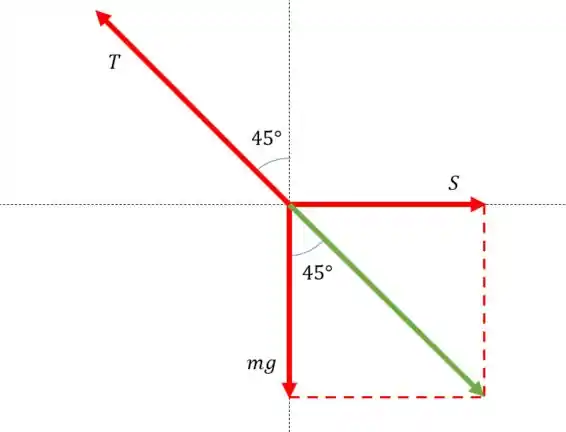
Esse ângulo só pode ser se e tiverem a mesma intensidade, olha só, se for maior que , então o ângulo é maior que , mas se for ao contrário, o ângulo é menor que .
Então o módulo de e são iguais.
Resposta
O módulo de e são iguais.