Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo - Ex.
6.45. Um viciado em movimentos circulares, com 80 kg de massa, está andando em uma roda-gigante que descreve uma circunferência vertical de 10 m de raio a uma velocidade escalar constante de 6,1 m/s. (a) Qual é o período do movimento? Qual é o módulo da força normal exercida pelo assento sobre o viciado quando ambos passam (b) pelo ponto mais alto da trajetória circular e (c) pelo ponto mais baixo?
Passo 1
Então a situação é a seguinte
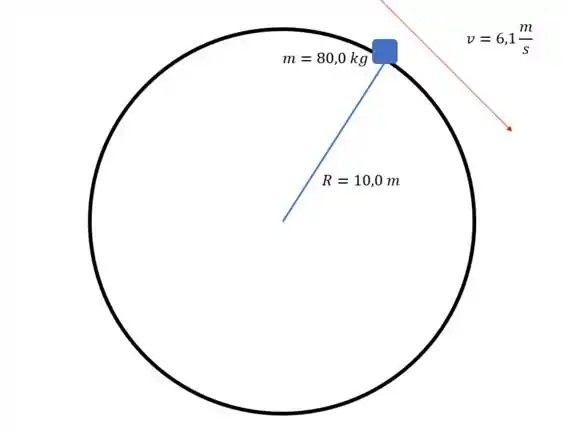
Vamos começar pelo item (a). Para calcular o período do movimento a gente tem que calcular quanto tempo demora para o viciado dar uma volta completa. Bom, a gente pode usar a seguinte relação
Bom, se a gente considerar que ele dá uma volta completa, a mesma equação fica o seguinte
Agora a gente pode isolar o período
Agora é só substituir os valores
Passo 2
Agora vamos para o item (b). Agora tem a ver com a força normal, bom, a força normal é a força de reação à força que o viciado exerce sobre o assento. No ponto mais alto da trajetória a gente tem essa condição
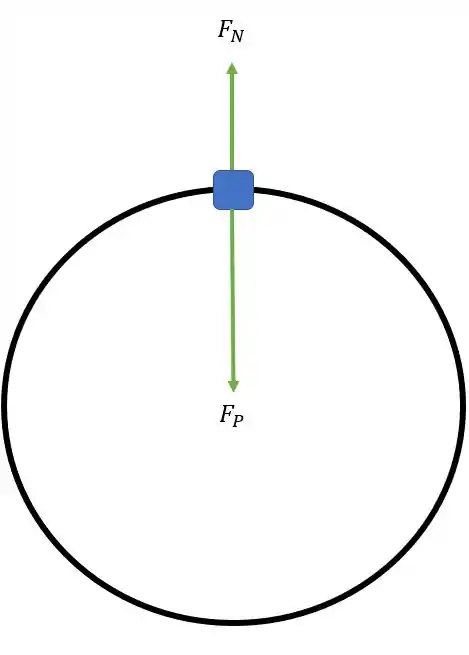
Tem a força peso apontando para baixo e a força normal aponta para cima. Bom, a força centrípeta é a resultante gerada por essas duas forças
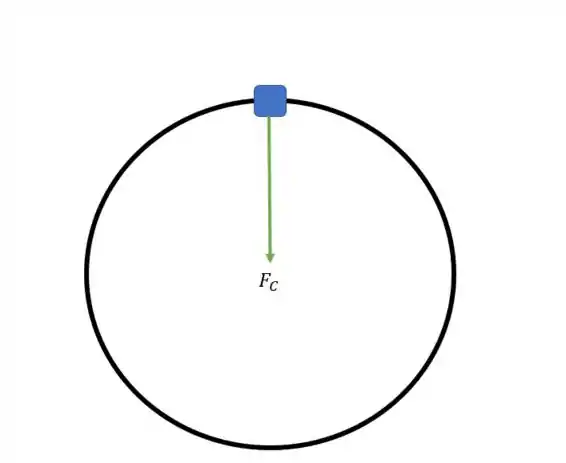
Então
Assumindo o sentido para cima como positivo.
Vamos isolar a força normal
Agora é só substituir
Agora a gente substitui os valores
Passo 3
Agora no item (c), a gente tem que calcular a força normal de novo, mas agora com o viciado no menor ponto do movimento.
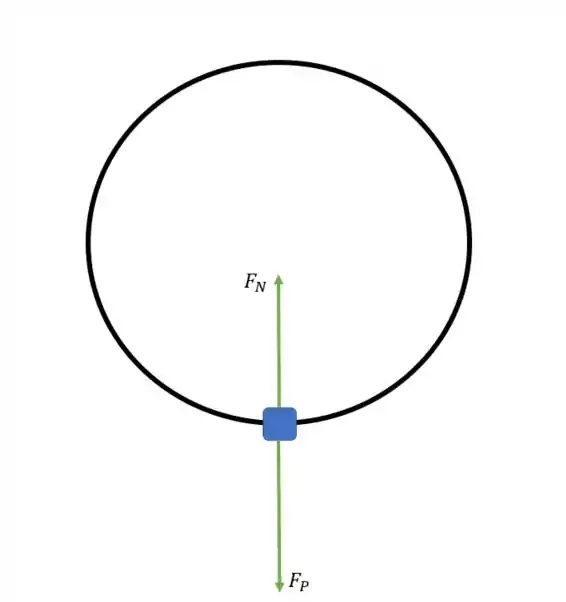
E a força centrípeta agora está assim
E agora a gente faz a mesma coisa que a gente fez no item anterior.
Agora é só substituir
Agora substituindo os valores