Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 8.Exercícios e Problemas - Ex. 2

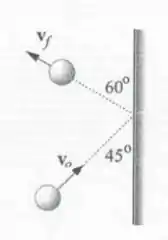
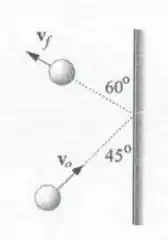
8.2E Uma bola de massa m colide com uma parede como se vê na figura 8.9. Sabendo-se que a bola perde meade de sua energia cinética na colisão, calcule o impulso que a parede transmite à bola, em termos de m v 0 .

Passo 1

Show de bolinhas meus amores, sabemos que o impulso pode ser medido como:

I = ∆ P

Maaaass, temos aqui uma colisão em duas dimensões, tal que nosso impulso também vai ser dividido em duas dimensões:

I x = ∆ P x ,     I y = ∆ P y

Passo 2

Então bora encontrar a variação do momento linear em cada dimensão, que ai poderemos expressar o impulso total. Saca só, dada nossa figura temos que no momento inicial, podemos dividir nossa velocidade como:

v 0 = v 0 sen ⁡ 45   î + v 0 cos ⁡ 45   j ^

v 0 = 2 2 v 0   î + 2 2 v 0   j ^

Já a velocidade final, será:

v f = - v f sen ⁡ 60   î + v f cos ⁡ 60   j ^

v f = - 3 2 v f   î + 1 2 v f   j ^

Passo 3

Logo as variações do momento linear em cada dimensão será:

∆ P x = - 3 2 v f m - 2 2 v 0 m

∆ P y = 1 2 v f m - 2 2 v 0 m

MAAAAASSS, a maior sagacidade de todas aqui é que o enunciado nos disse que a energia cinética final, é exatamene metade da energia cinética inicial.

K f = 1 2 K i

Logo:

1 2 m v f 2 = 1 2 1 2 m v 0 2

1 2 v f 2 = 1 4 v 0 2

Tal que:

v f = 2 2 v 0

Portanto, nossos momento lineares, serão:

∆ P x = - 3 2 2 2 v 0 m - 2 2 v 0 m = - 2 4 v 0 m 3 + 2

∆ P y = 1 2 2 2 v 0 m - 2 2 v 0 m = - 2 4 v 0 m

Dessa forma, nosso impulso pode ser escrito como:

I = I x   î + I y   j ^

E como acabamos de descobrir que:

I x = ∆ P x = - 2 4 v 0 m 3 + 2

I y = ∆ P y = - 2 4 v 0 m

Logo:

I = - 2 4 v 0 m 3 + 2   î + - 2 4 v 0 m   j ^

I = - 2 4 v 0 m 3 + 2   î + j ^

Resposta

I = - 2 4 v 0 m 3 + 2   î + j ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um vagão fechado em um pátio de manobras é colocado em movimento no topo de um morro artificial. O vagão desce silenciosamente e sem atrito sobre um trilho horizontal reto, onde se acopla com um vagão
Um trator de massa elevada está se movendo em uma estrada do campo. Em uma colisão perfeitamente inelástica, um pequeno carro esportivo bate na máquina por trás. ( i ) Qual veículo sofre maior variaçã
Uma bala de 10,0g é disparada e entra em um bloco de madeira de 200g em repouso sobre uma superfície horizontal. Após o impacto, o bloco desliza 8,00m antes de parar. Se o coeficiente de atrito entre
Um corpo de massa 3,00k g , movendo-se com uma velocidade inicial de 5,00 i ^m / s , colide e fica junto com um corpo de massa 2,00k g com uma velocidade inicial de – 3,00 j ^m / s . Encontre a veloci
Um punhado de argila pegajosa de massa m é atirado horizontalmente contra um bloco de madeira de massa M inicialmente em repouso sobre uma superfície horizontal. A argila adere ao bloco. Após o impact