Enunciado
Física - Okuno - Física para Ciências Biológicas e Biomédicas- Ed: 1º - Capítulo 9.Problemas - Ex. 10
9.10. A figura a seguir mostra a variação da energia potencial de uma molécula de ácido fluorídrico em função da distância r entre os átomos de hidrogênio e flúor.
a. Para quais valores de r os átomos se atraem ou repelem?
b. Qual o valor da energia potencial quando a distância entre os átomos for muito grande (r - > 00)?
Passo 1
Beleza vamos lá.
Tá legal, para o item (a) a gente não pode responder exatamente os valores de porque não sabemos exatamente a energia total na situação. Olha só, a energia é constante, então é uma reta. Vamos supor que a energia seja por exemplo.
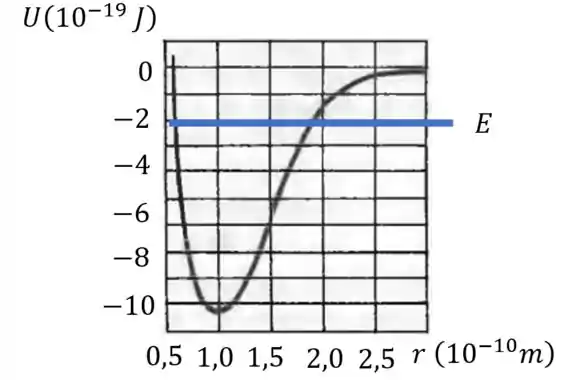
A energia cinética é aquilo que está entre a Energia total e a energia potencial. Por exemplo, quando a energia cinética é essa:
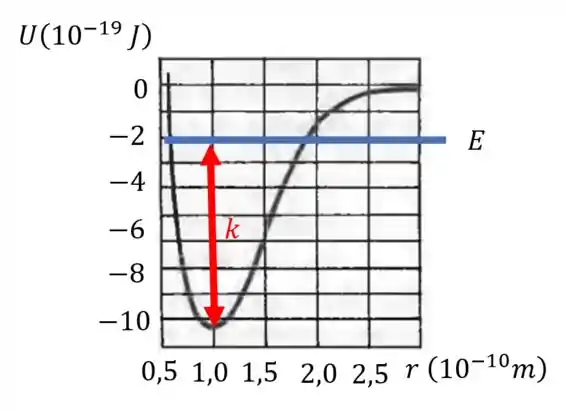
Tá legal, a gente sabe com certeza que se os átomos se atraem em algum momento . É o estado mais estável da molécula. Então os átomos param de se atrair para algum e algum .
Passo 2
Esses valores de dependem da energia total. Olha só, no nosso exemplo em que , quanto mais perto a curva de chega a partindo de , menor a energia cinética:
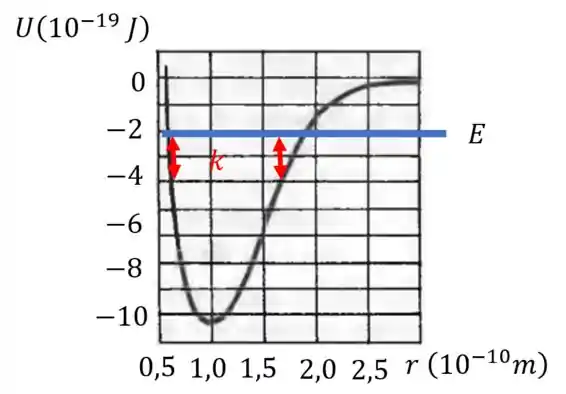
Quando a energia for maior que significa que a energia cinética é negativa (o que é um absurdo, então vamos descartar essa hipótese), ou então que houve um ganho de energia cinética. Esse ganho de energia cinética é justificado pelos átomos se afastando.
Então os valores de para os quais os átomos começam a se afastar são:
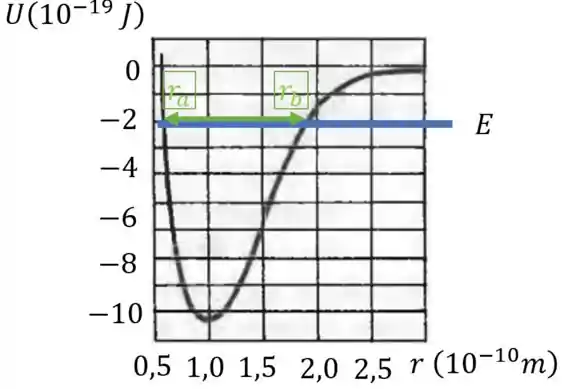
Em outras palavras são os valores de para os quais .
Passo 3
Agora vamos para o item (b).
Olha só, pela própria figura no gráfico podemos ver duas assíntotas. A primeira assíntota é vertical, para , e a outra assíntota é horizontal, para . Essa assíntota está em .
Então a energia potencial para quando vai para o infinito é . E isso faz sentido, por quanto mais os átomos se afastam menor é o potencial de energia que pode virar movimento, a atração entre os átomos é bem mais fraca.
Resposta
- São os valores de para os quais .
- .