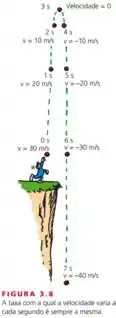
Alguém de pé junto à beira de um penhasco (como da Figura 3.8) atira uma bola verticalmente para cima com uma certa rapidez, e outra bola verticalmente para baixo com a mesma rapidez inicial. Se a resistência do ar for desprezível, que bola terá a maior rapidez ao atingir o solo?

Para essa solução vamos precisar determinar algumas coisas importantes:

Primeiro, precisamos saber a altura que a primeira bola alcança quando lançada verticalmente para cima com velocidade inicial .

Segundo, vamos calcular a velocidade da primeira bola no ponto . Depois poderemos achar a velocidade com que ela toca o solo.

Terceiro, definiremos a velocidade com que a segunda bola atinge o solo.

Assim, poderemos comparar nossos resultados e chegarmos em uma conclusão!

Agora que já definimos o roteiro para nossa solução completa, vamos analisar cada parte individualmente.

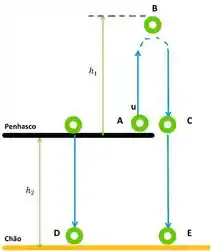
Figura 1 – Esquemático do Problema 66

Primeiramente, para a primeira bola atirada verticalmente para cima, ela caracteriza um movimento uniforme. E precisamos saber a altura máxima alcançada pela bola nessa trajetória. Observando a Figura 1, e desconsiderando a resistência do ar, podemos definir essa altura

Temos que a altura é e a velocidade da primeira bola no ponto (altura máxima) é .

Aplicando a terceira equação da cinemática do movimento, e a gravidade está agindo contra o movimento do corpo, então temos que:

E, resolvendo para

Para o segundo passo, vamos determinar a velocidade da primeira bola no ponto , sendo que esse ponto está na mesma altura que o penhasco. Para isso, tomaremos sendo a velocidade da primeira bola quando ela passa pelo ponto .

Aplicando a terceira equação da cinemática do movimento, e a gravidade está agindo a favor do movimento do corpo, então temos que:

Podemos substituir a expressão obtida no passo anterior para

Agora, a partir do penhasco, ambas as bolas (a primeira lançada verticalmente para cima e a segunda lançada diretamente para baixo) irão se mover para baixo com a mesma velocidade .

Podemos visualizar na Figura 1, a altura e temos que e são as velocidades da segunda e da primeira bola, respectivamente, no chão quando ambas atingem o mesmo.

Aplicando a terceira equação da cinemática do movimento para a segunda bola, e a gravidade está agindo a favor do movimento do corpo, então temos que:

Aplicando a terceira equação da cinemática do movimento para a primeira bola, e a gravidade está agindo a favor do movimento do corpo, então temos que: