Enunciado
Física - Cutnell e Johnson - Física- Ed: 9º - Capítulo 4.Problemas Adicionais - Ex. 110
Um alpinista, atravessa entre penhascos através de uma corda, e para depois para repouso. Ele pesa 535 N. Como mostrado abaixo, ele está mais próximo do penhasco da esquerda, com o resultado de que as tensões do lado esquerdo e direito não são as mesmas. Encontre a tensão da corda na parte da esquerda e direta.
Passo 1
E aí gente, tudo bem? Essa questão a gente vai precisar usar os conceitos fundamentais!!
Considerando que o alpinista está em repouso, ela está em equilíbrio e a força resultante deve ser zero.
Vamos fazer um diagrama de corpo livre aqui!!
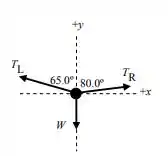
Vamos fazer um balanço de forças na direção x e y:
Podemos escrever essas equações em função de
Passo 2
Substituindo o resultado do passo (1) na segunda equação, temos que:
Usando esse resultando na equação de TR temos que:
Passo 3
Bem, uma vez conhecido o peso, temos que: