Quando uma amostra de prata é irradiada com nêutrons por um curto período de tempo, dois isótopos radioativos se formam: (), com uma taxa de decaimento inicial de , e (), com uma taxa de decaimento inicial de . Faça um gráfico semilog semelhante ao da Fig. 42-9 mostrando a taxa de decaimento global da amostra em função do tempo entre e . A Fig. 42-9 foi usada para ilustrar um método de determinação da meia-vida de um único isótopo radioativo. Dado apenas o gráfico da taxa de decaimento global do sistema de dois isótopos, mostre que é possível analisa-lo e determinar as meias-vidas dos dois radioisótopos.
Passo 1
Bom, sabemos que a taxa de decaimento também é conhecida por atividade e que a atividade resultante é a soma das atividades de cada núcleo:
onde e . Além disso:
Assim,
Passo 2
Tomando o log dos dois lados da equação:
Plotando o gráfico para :
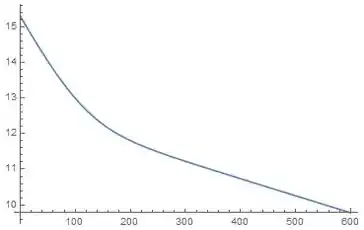
Resposta
Esboço de gráfico.