Um anel m com 5,0 kg de massa desliza sobre um arco metálico liso ABC (Fig. 8.24) moldado na forma de um arco de círculo com 1,20 m de raio. Há duas forças agindo sobre o corpo, F e F', cujos módulos são, respectivamente, 40 N e 150 N. A força F permanece tangente ao círculo. A força F' age numa direção constante que forma um ângulo de 30 graus com a horizontal. Calcule o trabalho total realizado pelo sistema de forças que age no corpo quando ele se move de A para B e de A para C.
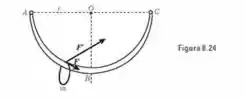
Passo 1
Fala galeraa, tudo bem??
Em questões assim, nós precisamos analisar o diagrama de forças do caso do exercício. Ou seja, vamos entender melhor cada uma das forças e suas componentes atuando no arco. Como temos o anel deslizando no (e pendente ao) arco, já podemos dizer que há influência de uma força peso, que age no arco, vinda da interação arco-anel, certo? Ok, vamos chamar essa força de P e, por enquanto, guardar essa informação em um potinho hahahaha.
Passo 2
Agora, sabemos da influência de mais duas forças: a força F e a força F’. A força F é tangente ao arco. Se formos observar a figura do enunciado, podemos dizer que ela é uma componente da força peso, concordam? Já que temos a força peso apontando para baixo, vamos tirar ela do potinho e entender que a força F pode ser encontrada da seguinte maneira:
F = Fy = P * cos θ
Passo 3
Certo, por último, nós temos a força F’, que age formando um ângulo de 30 graus com a horizontal.
Assim, para organizar melhor nossa cabeça, vamos entender o diagrama:
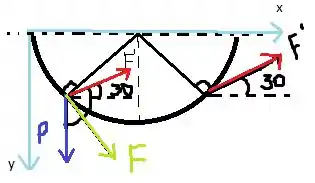
Temos a força P em azul, a força F em verde e a força F’ em vermelho. O eixo x,y em azul. Vamos considerar o eixo y apontando para baixo, para facilitar nossas contas, ok?
Passo 4
Agora, vamos relembrar um pouquinho de trabalho?? O trabalho é uma grandeza física que mede a transferência de energia e é dado pela transferência de força ao longo de um deslocamento. Assim, podemos dizer que o trabalho pode ser dado pelo produto escalar entre o deslocamento e a força realizada. Ou seja:
Neste caso, como precisamos considerar cada movimento realizado pelo anel durante todo seu percurso. Além disso, o deslocamento realizado pelo anel será em função do raio do círculo, certo? Então, vamos utilizar a definição de trabalho por:
, em que ds é o deslocamento delta do arco todo. Como temos o arco todo composto por várias componentes, sabemos que o eixo x e o eixo y serão também decomposições, ou seja:
Como ds é a composição de dx e dy, então:
Passo 5
Certo, agora conseguimos, então, voltar ao trabalho realizado pela força F ao anel percorrer o arco:
Passo 6
O segundo trabalho, realizado pelo movimento angular do corpo, será dado por:
Passo 7
Por fim, o terceiro trabalho, realizado em função de F’, será:
Uma observação muito importante é que, se olharmos o desenho, teremos um ângulo de 180 graus entre F’ e o eixo x, assim, o ângulo em questão será de 120-𝜽, certo? Assim, seguindo a conta acima teremos:
Assim, temos que:
Passo 8
Pronto, agora, precisamos somar todos os trabalhos encontrados, para calcularmos o trabalho total realizado de A até B:
Substituindo os valores dados no enunciado, temos:
Logo, concluímos, finalmente (e pedindo socorro hahahaha) que o trabalho de A até B, é de 203,4 J.
Passo 9
Porém, não acabamos ainda! O exercício ainda nos pede o trabalho de A até C! Para tal, teremos o mesmo esquema, mas, em relação ao ângulo entre A e C, ao invés de A e B. Como podemos ver no diagrama, o ângulo será de , então:
Realizando os cálculos, teremos:
Agora sim!! Finalmente, encontramos que o trabalho de A até C é de 266 J!
Resposta
Trabalho de A a B:
Trabalho de A a C: