Um astronauta em órbita a uma altura de 240 km disse que podia identificar as casas da cidade enquanto passava sobre elas. Pode-se dar crédito a isso? Suponha e o diâmetro da pupila igual a 1 mm.
Passo 1
Da teoria temos: , onde b = diâmetro dos olhos [m]
Substituindo os valores do enunciado:
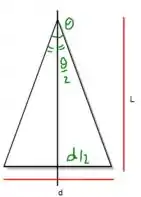
Passo 2
Fazendo e sabendo que L = 240km = 240000m e d=1mm
Substituindo achamos:
D = 161,04m
Passo 3
Logo, ele só enxergará se as casas tiverem o comprimento de pelo menos 161,04m
Resposta
Logo, ele só enxergará se as casas tiverem o comprimento de pelo menos 161,04m