Um avião de resgate voa horizontalmente a uma velocidade constante em busca de um barco quebrado. Quando o avião está diretamente acima do barco, seus tripulantes buzinam bem alto. Até o momento em que o detector de som do avião localiza o som, o avião percorreu uma distância igual à metade da sua altura acima do oceano. Supondo que demore 2,00 s para o som chegar ao avião, determine (a) a velocidade do avião; (b) sua altitude.
Passo 1
Helloooou pessoalll, bora pra mais um??
Encoxxtaaa!!
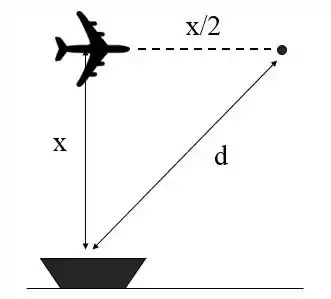
Sabemos que os tripulantes do barco buzinam quando o avião se encontra exatamente acima deles, a uma distância x. O detector de som do avião detecta a buzina após o avião percorrer uma distância horizontal x/2. Como ilustrado na figura.
Passo 2
Portanto, a distância percorrida pelo som da buzina até atingir o detector do avião correspondente à hipotenusa do triângulo indicado na figura. Assim:
Passo 3
Dado que a velocidade do som no ar é de e que foi detectado após um tempo . Então, podemos afirmar que:
Manipulando essa expressão, temos que
Passo 4
- Com base na imagem do passo 1, a velocidade do avião é:
- De acordo com a imagem do passo 1, a altitude do avião corresponde a .
Passo 5
Resposta
- A velocidade do avião é de 153,4 m/s.
- x = 613,6 m.