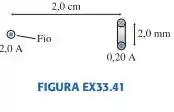
Com base na FIGURA EX33.41, responda:

1. Qual é o módulo do torque exercido sobre a espira de corrente?
2. Qual é a orientação de equilíbrio da espira?

Faaaaaala, galera... Tranquileba??

Sabemos que o torque magnético é:

E pela definição de produto vetorial, podemos fazer:

Sabemos que o momento de dipolo magnético é:

Onde A é a área e I a corrente.

E para o campo magnético produzido pelo fio a uma distância é um pouco menos fácil, mas bora lá:

Sabemos que a lei de Bio-Savart é:

E para um fio muito longo, como:

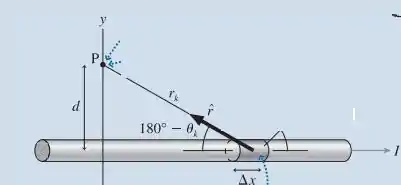
Temos que:

E:

Assim:

Sendo um fio muito longo, logo:

Logo:

De integral simples. Assim, o campo elétrico a uma distância d sobre um fio longo que passa uma corrente é:

Ufaaa. Agora temos que:

E já estamos com o pé na resposta, não?

Bora pro próximo passo!