Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 5.Problemas - Ex. 12

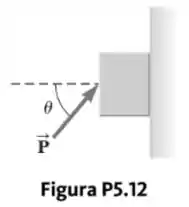
Um bloco de 3,00   k g é empurrado contra uma parede por uma força   P →   que forma um ângulo θ   =   50,0 ° com a horizontal, como mostra a Figura P5.12. O coeficiente de atrito estático entre o bloco e a parede é 0,250 .

  1. Determine os valores possíveis para o módulo   P → que permitem que o bloco permaneça parado.
  2. Descreva o que acontece se | P → | tiver um valor maior e o que acontece se for menor.
  3. Repita as partes (a) e (b) considerando que a força forma um ângulo de θ =   13,0 ° com a horizontal.

Passo 1

E aiii gente, tudo bom com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo e bora!

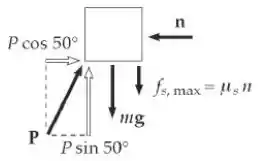
Letra a:

Para encontrar o valor máximo possível de P, imagine um movimento para cima iminente como o caso 1. Sendo ∑ F x = 0 :

P c o s ⁡ 50.0 ∘ - n = 0

Com f s , m a x = μ s n :

f s , m a x = μ s P c o s ⁡ 50.0 ∘ = 0.250 ( 0.643 ) P = 0.161 P

Sendo ∑ F y = 0 :

Psin ⁡ 50.0 ∘ - 0.161 P - ( 3.00 k g ) 9.80 m s 2 = 0 P m a x = 48.6 N

Para encontrar o valor mínimo possível de P, considere o movimento iminente para baixo. Como no caso 1, f s , m a x = 0.161 P , então fazendo ∑ F y = 0 :

P s i n ⁡ 50.0 ∘ + 0.161 P - ( 3.00 k g ) 9.80 m s 2 = 0 P m i n = 31.7 N

Passo 2

Letra b:

Se P> 48.6 N, o bloco desliza para cima na parede. Se P

Passo 3

Letra c:

Repetimos o cálculo como na parte (a) com o novo ângulo. Considere o movimento para cima iminente como caso 1. Seja ∑ F x = 0 :  

Pcos ⁡ 13 ∘ - n = 0

f s , m a x = μ s n :                     f s , m a x = μ s P c o s ⁡ 13 ∘

f s , m a x = 0.250 ( 0.974 ) P = 0.244 P

Sendo ∑ F y = 0 :

Psin ⁡ 13 ∘ - 0.244 P - 3.00 k g 9.80 m s 2 = 0

P m a x = - 1580 N

O empurrão não pode ser realmente negativo. Por maior ou menor que seja, não pode produzir movimento para cima. Para encontrar o mínimo valor de P possível, considere um movimento para baixo iminente. Como no caso 1, f s , m a x = 0.244 P . Sendo ∑ F y = 0 :

P s i n ⁡ 13 ∘ + 0.244 P - ( 3.00 k g ) 9.80 m / s 2 = 0 P m i n = 62.7 N

O bloco não pode deslizar para cima pela parede. Se P

Resposta

  1. P m a x = 48.6 N , P m i n = 31.7 N
  2. Se P> 48.6 N, o bloco desliza para cima na parede. Se P
  3. O bloco não pode deslizar para cima pela parede. Se P
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um carro está viajando a 50,0m i / h em uma rodovia horizontal. Se o coeficiente de atrito estático entre a estrada e os pneus em um dia chuvoso é 0,100 , qual é a distância mínima em que o carro para
A pessoa na Figura P5.6 pesa 170l b . Como visto de frente, cada muleta faz um ângulo de 22,0 ° com a vertical. Metade do peso da pessoa é suportada pelas muletas. A outra é suportada pelas forças ver
Antes de 1960, as pessoas acreditavam que o coeficiente de atrito estático máximo atingível para um pneu de automóvel em uma rodovia era μ S=1 . Por volta de 1962, três empresas desenvolveram, de form
Por que a seguinte situação é impossível? Uma torradeira de 1,30k g não está ligada na tomada. O coeficiente de atrito estático entre ela e uma bancada horizontal é 0,350 . Para fazer a torradeira com