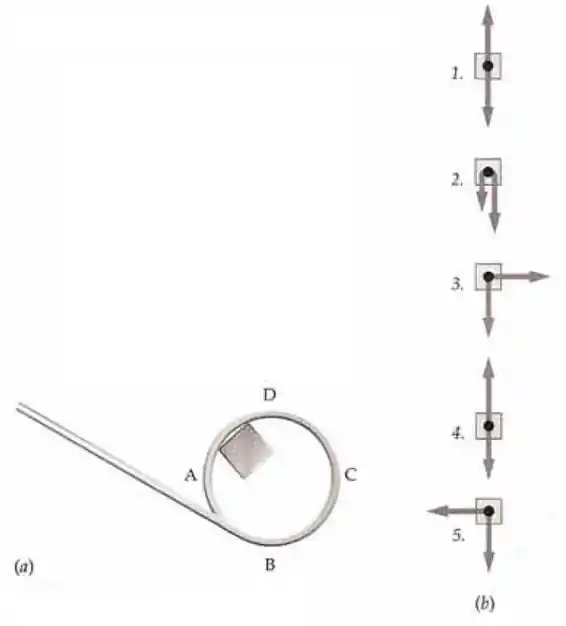
Um bloco escorrega sobre uma superfície sem atrito ao longo do trilho de perfil circular da figura a. O movimento do bloco é rápido o suficiente para impedir que ele perca contato com o trilho. Relacione os pontos ao longo do caminho com os respectivos diagramas de corpo livre da figura b.

Vamos olhar para o ponto A. A força gravitacional precisa apontar para baixo e perpendicularmente ao trilho.

E como aponta para baixo, a única forma de termos uma componente da nossa força resultante apontando para o centro da trajetória é se a força normal apontar para dentro do circulo.

Ficamos assim:

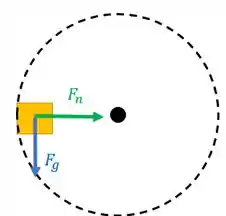
Esse é o diagrama 3.

Olhando para B, a força peso precisa estar para baixo e precisa ser normal ao trilho.

A gente precisa que a resultante tenha uma componente apontando para o centro do circulo, então vamos colocar apontando para dentro do circulo:

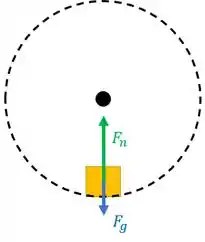
E percebe uma coisa. A gente PRECISA ter uma resultante para dentro do circulo. Então precisa ser maior que , para que a força resultante esteja no sentido de .

Isso aparece no diagrama 4.

Aqui na C temos uma situação muito parecida com a A. A força peso aponta para baixo. E a normal (sempre perpendicular ao trilho) deve apontar para dentro do circulo para que haja componente da resultante apontando para o centro dele.

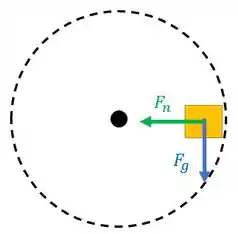
Isso aparece no diagrama 5.

Por fim, temos que no ponto D, a força peso aponta para baixo (sempre) e a normal precisa também apontar para dentro do circulo.

Como a normal é perpendicular ao trilho e aponta para dentro do circulo, ela vai apontar para baixo nesse caso.

Desse modo há tranquilamente uma componente da resultante apontando para o centro do circulo pois as duas forças apontam para baixo.

Isso acontece no diagrama 2.