Para treinar astronautas que trabalharão na Lua, onde a aceleração da gravidade é apenas cerca de 1/6 do que vale na Terra, a NASA submerge-os em um tanque de água. Se uma astronauta levando mochila, unidade de ar condicionado, suprimento de oxigênio e mais algum equipamento tem uma massa total de 250 kg, determine as seguintes quantidades. (a) Seu peso, incluindo mochila etc. na Terra, (b) seu peso na Lua, (c) a necessária força de empuxo para cima exercida pela água durante o treinamento para se ter, em Terra, o ambiente da Lua.

b) Para obter o peso na Lua podemos usar a mesma fórmulnha da força peso:

A diferença é que aqui temos a aceleração da gravidade na lua. O enunciado diz que ela é da gravidade na Terra, então a gente pode fazer:

Agora, podemos usar a fórmulinha deboas:

Substituindo os dados:

c) Queremos que o astronauta tenha aparentemente o peso que ele teria na Lua mas estando na Terra. E o que é o peso? Ele é uma força que nos puxa para baixo.

Então, uma forma de simular o peso da lua aqui na Terra seria ter a força resultante sobre o astronauta para baixo de .

E como isso pode ser feito? A NASA faz isso colocando esse cara dentro da água. Por que? Porque a água exerce uma força voltada para cima sobre o astronauta chamada de empuxo . Assim a força resultante sobre ele para baixo diminui.

Para calcular a força resultante a gente só precisa somar os módulos das forças que agem sobre o astronauta na direção vertical respeitando seus sentidos. Essa é a situação que a gente tem:

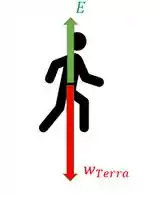
Considerando o sentido positivo para baixo, nossa força resultante pode ser calculada assim:

Só que a gente quer que essa força resultante seja igual ao peso dele na lua, então temos:

Isolando quem a gente quer achar e substituindo nossos resutados: