Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo - Ex.
O bloco da Fig. 6-56 possui massa e o bloco possui massa . O coeficiente de atrito cinético entre o bloco e o plano horizontal é . O ângulo do plano inclinado sem atrito é . A polia serve apenas para mudar a direção do fio que liga os blocos. O fio possui massa desprezível. Determine :
(a)a tensão do fio e (b) o módulo da aceleração dos blocos .
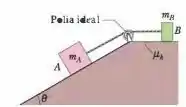
Passo 1
Opa!! Vamos começar dando uma olhada nos diagramas de corpo livre para entendermos melhor o problema, começando pelo Bloco A, que desce a rampa.
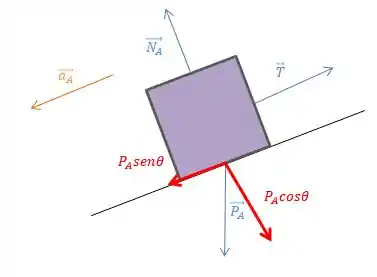
E agora para o bloco o Bloco B:
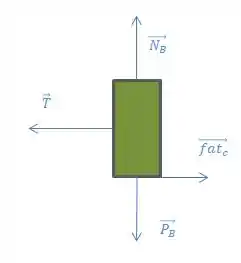
Como aqui temos um sistema que se move junto, podemos dizer que as acelerações dos blocos vão ser iguais em módulo a aceleração do sistema:
Agora podemos aplicar a Segunda Lei de Newton ao bloco A e ao bloco B.
Mas se liga, que como aqui temos um sistema, precisamos considerar a direção da aceleração como sendo a nossa direção positiva, beleza?
Bloco A – Eixo X (ao longo do plano).
Bloco B – Eixo X
Beleza?!
Nós sabemos que a força de atrito cinética no bloco B é dada por
E para encontrar a Normal no bloco B, faremos a primeira lei de Newton para o eixo Y, afinal ele não irá ter aceleração no eixo Y.
Bloco B – Eixo Y
Sendo assim, temos que a força de atrito no Bloco B, será:
Passo 2
Podemos substituir por seu valor na equação da segunda lei para o Bloco B, obtemos assim um sistema de equações.
E substituindo os valores que foram dados no enunciado, teremos:
Agora só precisamos resolver esse sistema de equações, para isso, vou colocar em evidência a tração na segunda equação:
E substituindo na primeira equação, teremos:
E portanto a aceleração do sistema (e dos blocos) será:
Que com 2 algarismos significativos ficará:
E para encontrar a tração, é só substituir a aceleração em qualquer uma das equações do sistema, vou substituir na segunda equação:
E com 2 algarismos significativos ficará:
Resposta
Tranquilo pessoal??? Bora resolver mais questões então!!!