Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo - Ex.
O bloco na Fig. 7-9a está sobre uma superfície horizontal sem atrito e a constante elástica é . Inicialmente, a mola está relaxada e o bloco está parado no ponto . Uma força com módulo constante de é aplicada ao bloco, puxando-o no sentido positivo do eixo e alongando a mola até o bloco parar. Quando este ponto é atingido, qual é (a) a posição do bloco, (b) o trabalho realizado sobre o bloco pela força aplicada e (c) o trabalho realizado sobre o bloco pela força elástica? Durante o deslocamento do bloco, qual é (d) a posição do bloco na qual a energia cinética é máxima e (e) o valor desta energia cinética máxima?
Passo 1
Falaa galera, tudo certo? Aqui a gente vai trabalhar com conservação da energia, sendo assim vamos encontrar todas as energias necessárias pra resolver tudo o que a gente precisa, ok?
Vamos começar, dando uma lembrada aqui na definição de trabalho:
E o trabalho da força elástica é dado por:
Sendo assim , temos por equilíbrio:
E substituindo:
Resolvendo pra x diferente de zero a gente tem:
Em outras palavras para o item a.
Passo 2
Pro item b, vamos calcular o trabalho realizado pela força aplicada , que por sua vez é dado pela relação :
Passo 3
Já para o item c. o trabalho realizado pela mola percorre a mesma distância e na mesma direção do trabalho realizado pela força aplicada, porém sentidos opostos . Sendo assim :
.
Passo 4
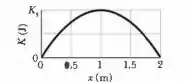
O item d, pede que calculemos a posição para a energia cinética máxima.
Então galera , considerando as energias cinéticas final e inicial , obtemos que :
Para acharmos o ponto onde a energia cinética K é máxima , devemos derivar em relação a e igualar a equação que acharmos a zero . Sendo assim :
Note que também é o ponto no qual a força resultante é nula.
Passo 5
Enfim para o item e. vamos calcular a energia cinética máxima substituindo o valor de na expressão da energia cinética .Sendo assim :
Resposta
Tranquilo galera??? Bora resolver mais questões então!!!!!!