Um bloco é pressionado contra uma parede vertical por uma força, como mostra o desenho. Esta força pode empurrar o bloco para cima a uma velocidade constante ou permitir que ele deslize para baixo a uma velocidade constante. A magnitude da força é diferente nos dois casos, enquanto o ângulo direcional é o mesmo. Existe atrito cinético entre o bloco e a parede, e o coeficiente de atrito cinético é 0,250. O peso do bloco é 39,0 N, e o ângulo direcional para o a força é 30,0. Determine a magnitude de quando o bloco desliza (a) pela parede e (b) descer pela parede.
Passo 1
Oii, tudo bem?
Vamos lá resolver mais um problema desse capítulo, tenta fazer antes e depois vem conferir aqui com a gente tá?!
A figura dada no problema é a seguinte
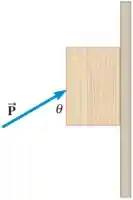
Passo 2
O bloco está em equilíbrio em cada caso, porque o bloco tem uma constante velocidade e não está acelerando. Uma aceleração zero é a marca registrada do equilíbrio. No equilíbrio, a força resultante é zero (ou seja, o equilíbrio das forças a zero)
A gente pode calcular a magnitude da força de empuxo, usando o equilíbrio de forças para as direções.
Passo 3
Observe que a direção da força de atrito () não é a mesma em cada caso. A força de atrito sempre se opõe à superfície do bloco e a parede.
Portanto, quando o bloco desliza para cima, a força de atrito aponta para baixo. Quando o bloco desliza para baixo, a força de atrito aponta para cima.
Essas direções são mostradas nos diagramas de corpo livre para os dois casos. Nesses desenhos é o peso do bloco e é a força de atrito cinética.
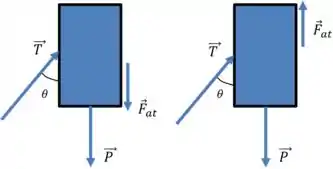
Onde, os eixos positivos são para a direita e para cima. O diagrama da esquerda é para o movimento para cima e o da direita é para o movimento para baixo.
Passo 4
Em cada caso, a magnitude da força de atrito () é a mesma, mas a direção é diferente. E é dado pela equação abaixo
onde é o coeficiente de atrito cinético e é a força normal.
O coeficiente de atrito cinético () não depende da direção do movimento. Além disso, a magnitude da força normal em cada caso é o componente de a força de empuxo perpendicular à parede, ou seja
Passo 5
Podemos fazer o equilíbrio de forças na direção , para cima e para baixo.
Para cima:
Para baixo:
Passo 6
Para a força de atrito como vimos
E
Logo
Passo 7
Substituindo nas equações para movimento para cima e para baixo, temos
Para cima:
Para baixo:
Passo 8
Resolvendo cada caso para , temos que
a. Para cima:
b. Para baixo: