Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 27.Exercício - Ex. 46

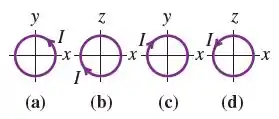
Uma bobina circular de área A   possui N espiras e pode girar em torno de um diâmetro que coincide com o eixo O x . Uma corrente I   está circulando na bobina. Existe um campo magnético no sentido positivo do eixo O y . Determine o módulo, a direção e o sentido do torque e o valor de energia potencial U , como indicado na Equação U = μ _ ⋅ B _ , quando a bobina estiver orientada nas posições indicadas de (a) até (d), na Figura E27.55.

Passo 1

O torque é dado pela expressão:

τ _ = μ _ × B _

E a energia potencial:

U = - μ _ ⋅ B _

O momento magnético da espira é:

μ _ = i A   n ^

Pelo enunciado:

B _ = B   j ^

Passo 2

letra a)

No primeiro desenho temos que o vetor normal está no sentido positivo do eixo z .

Logo:

μ _ = i A   k ^

Então o torque será:

τ _ = i A   k ^ × B   j ^

τ _ = i A B - i ^

E a energia potencial será:

U = - i A   k ^ ⋅ B   j ^

U = 0

Passo 3

letra b)

No segundo desenho temos que o vetor normal está no sentido positivo do eixo y .

Logo:

μ _ = i A   j ^

Então o torque será:

τ _ = i A     j ^ × B   j ^

τ _ = 0

E a energia potencial será:

U = - i A     j ^ ⋅ B   j ^

U = - i A B

Passo 4

letra c)

No terceiro desenho temos que o vetor normal está no sentido negativo do eixo z .

Logo:

μ _ = i A   - k ^

Então o torque será:

τ _ = i A   - k ^ × B   j ^

τ _ = i A B i ^

E a energia potencial será:

U = - - i A   k ^ ⋅ B   j ^

U = 0

Passo 5

letra b)

No último desenho temos que o vetor normal está no sentido negativo do eixo y .

Logo:

μ _ = i A -   j ^

Então o torque será:

τ _ = i A -   j ^ × B   j ^

τ _ = 0

E a energia potencial será:

U = - - i A     j ^ ⋅ B   j ^

U = i A B

Resposta

letra a) τ _ = i A B - i ^ , U = 0

letra b) τ _ = 0 , U = - i A B

letra c) τ _ = i A B i ^ , U = 0

letra d) τ _ = 0 , U = i A B

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O solenoide é removido do recipiente e depois usado em um novo local, onde o campo magnético da Terra é de 50 μ T e aponta horizontalmente. Uma amostra das bactérias é colocada no centro do solenoide,
Como estagiário em um laboratório de pesquisa, você recebe um solenoide longo que possui dois enrolamentos separados e próximos, no mesmo sentido, sobre a mesma forma cilíndrica oca. Você precisa dete
Um fio condutor de comprimento fixo L pode ser enrolado em N voltas circulares e utilizado com uma armadura para um gerador. Para obter a maior fem, que valor de N deveria ser escolhido?
Um fio é dobrado em três segmentos circulares de raio r = 10,4c m como mostrado na Fig. 34-55. Cada segmento é formado de 1 / 4 de círculo, o segmento a b no plano x y , o segmento b c no plano y z e
Na Fig. 29-42, dois fios retilíneos longos, separados por uma distância d = 16,0c m , conduzem correntes i 1 = 3,61m A e i 2 = 3,00 i 1 dirigidas para fora do papel. (a) Em que ponto do eixo x ∘ campo