Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 9.Exercícios e Problemas - Ex. 12
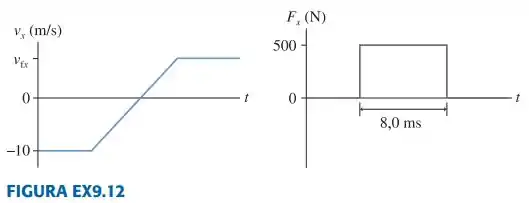
Uma bola de 250 g colide com uma parede. A FIGURA EX9.12 mostra a velocidade da bola e a força exercida sobre ela pela parede. Quanto vale , a velocidade de ricocheteio da bola?
Passo 1
O teorema impulso-momentum correlaciona a força aplicada por um determinado tempo (impulso) em um corpo com a variação da sua velocidade, que está ligada a seu momentum.
A seguinte equação descreve o teorema:
Onde e são respectivamente o impulso e o momentum do corpo. Essa equação pode ser reescrita em termo de escalares, assim:
Onde , t, e e são, respectivamente, a força aplicada, o tempo de ação da força, a massa do corpo e as velocidades inicial e final do corpo no intervalo de tempo avaliado.
Passo 2
Aqui, temos dois gráficos que nos dão as informações necessárias pra descobrirmos nossa incógnita,a velocidade de ricocheteio.
Pelo primeiro gráfico, temos que a velocidade inicial . No segundo gráfico, pela área entre a curva e o eixo temos o valor do impulso aplicado na bola. Basta calcular a área do retângulo:
Repara que passamos milissegundos pra segundos. Precisamos das unidades todas no sistema internacional (Si).
Feito isso, podemos aplicar na equação do teorema impulso-momentum, que vamos ter como única incógnita o valor de . Teremos:
Passo 3
Essa então é a velocidade de ricocheteio da bola!