Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo - Ex.
Uma bola de aço de massa está presa em uma extremidade de uma corda de de comprimento. A outra extremidade está fixa. A bola é liberada quando a corda está na horizontal (Fig. 9-65). Na parte mais baixa da trajetória, a bola se choca com um bloco de metal de inicialmente em repouso sobre uma superfície sem atrito. A colisão é elástica. Determine (a) a velocidade escalar da bola e (b) a velocidade escalar do bloco, ambas imediatamente após a colisão.
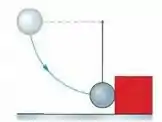
Passo 1
Bom pessoal , em primeiro lugar, calculamos a velocidade da bola imediatamente antes da colisão , ou seja , no ponto mais baixo da trajetória.
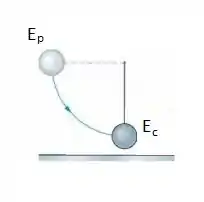
Note que no início do movimento temos uma energia potencial gravitacional e no instante antes da colisão temos uma energia cinética, de acordo com a lei de conservação da energia mecânica, temos que :
Isolando a velocidade na equação obtemos:
Vamos substituir na equação os valores que conhecemos, g= 9,8 e h=0,7(não esquecer de passar para metros).
Passo 2
Vamos agora analisar a colisão elástica:
Usando a fórmula da colisão elástica frontal temos que:
Aqui consideramos a bola como o corpo 1 e o bloco como o corpo 2, podemos ver que a velocidade inicial do bloco é zero, logo
Substituindo isso, teremos:
Passo 3
Como já sabemos as massas e a velocidade podemos descobrir a velocidade escalar final:
O que significa que a velocidade escalar final da bola é , e como deu negativo, sabemos que essa velocidade será para a esquerda.
Passo 4
Finalmente, para calcularmos a velocidade final do bloco usamos a fórmula :
Resposta
Tranquilo galera? Bora resolver mais questões então ☺