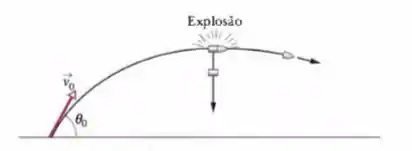
Um canhão dispara um projétil com uma velocidade inicial e um ângulo com a horizontal. No ponto mais alto da trajetória, o projétil explode em dois fragmentos de massas iguais (Fig. 9-42). Um fragmento, cuja velocidade imediatamente após a colisão é zero, cai verticalmente. A que distância do canhão cai o outro fragmento, supondo que o terreno é plano e que a resistência do ar pode ser desprezada?
Passo 1
Primeiro, vamos determinar a velocidade e a posição do projétil instantaneamente antes da explosão. Para isso, devemos lembrar que no ponto mais alto, a componente da velocidade é nula, lembrando que a componente da velocidade em função do tempo é:
Assim, no ponto mais alto:
Isolando :
Passo 2
Com o tempo em mãos, podemos calculcar a posição da projétil no ponto da explosão. Usando a função horária da posição para determinar a posição em :
Substituindo os valores:
E a função da posição para um MRU para determinar a posição em :
Substituindo os valores:
Assim, a posição onde ocorre a explosão é .
Passo 3
Lembrando que no eixo não há aceleração, então a velocidade em é constante:
Portanto, a velocidade do projétil no momento da explosão é
Passo 4
Como ocorreu uma explosão, podemos aplicar a conservação do momento linear entre os instantes imediatamente antes da explosão e imediatamente depois, assim:
Como o projétil foi dividido em pedaços iguais e que um pedaço possui velocidade nula após a explosão, então:
Calculando para o eixo :
Isolando :
E, agora, para o eixo :
Passo 5
Agora, devemos analisar apenas o movimento do segundo fragmento. Como a componente da velocidade é nula e a aceleração é a gravidade, então:
Onde o já foi calculado, que é a posição onde ocorre a explosão, . Assim, calculando o tempo que ele chega em :
Isolando :
Passo 6
Calculado agora a componente posição do fragmento do projétil no instante , lembrando que este é um MRU, portanto:
Com e :
Portanto, o projétil cai a do canhão.