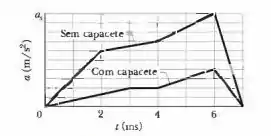
Quando uma bola de futebol é chutada na direção de um jogador e o jogador desvia de cabeça, a aceleração da cabeça durante a colisão pode ser relativamente grande. A Fig 2-35 mostra a aceleração da cabeça de um jogador de futebol sem e com capacete, a partir do repouso. A escala vertical é definida por . Qual é a diferença entre a velocidade da cabeça sem e com o capacete no instante ?
Passo 1
Falaa galerinha, bora resolver esse problema de cinemática?
Para começar vamos lembrar a definição de velocidade:
,
Lembrando que a integral é a área abaixo da curva, porém pra esse tipo de gráfico vale mais a pena a gente calcular as áreas do jeito tradicional.
Eu prometo á vocês que as fórmulas que a gente vai usar são só essas aqui:
O exercício nos deu o gráfico da aceleração em duas ocasiões: uma com capacete (gráfico menor) e outra sem capacete (gráfico maior). Então, a partir das áreas dos gráficos, conseguimos extrair o valor da velocidade em cada instante de tempo.
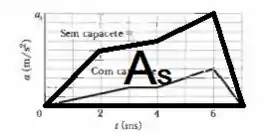
Assim, podemos encontrar a diferença entre a velocidade da cabeça sem e com capacete no instante () calculando a diferença dessas áreas ().
Atenção as unidades! O eixo da aceleração (eixo ) está em e o eixo do tempo (eixo ) está em , logo, precisamos consertar as unidades. Para isso, multiplicaremos o eixo do tempo por para transformar de milissegundo para segundo.
Passo 2
Vamos iniciar calculando a velocidade da cabeça sem capacete (), para isso, calcularemos a área .
Neste caso, dividiremos a área total em dois triângulo e dois trapézios.
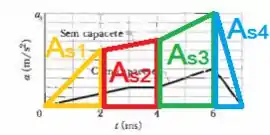
Primeira divisão (triângulo amarelo):
Segunda divisão (trapézio vermelho):
Terceira divisão (trapézio verde):
Quarta divisão (triângulo azul):
Assim, encontramos a velocidade da cabeça sem capacete () no instante somando as áreas acima:
Passo 3
Agora, faremos de maneira análoga para calcular a velocidade da cabeça com capacete (). A área que calcularemos é:
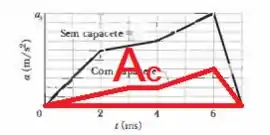
Para este, calcularemos as áreas de dois triângulos, um retângulo e um trapézio.
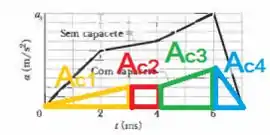
Primeira divisão (triângulo amarelo):
Segunda divisão (retângulo vermelho):
Terceira divisão (trapézio verde):
Quarta divisão (triângulo azul):
Assim, a velocidade da cabeça com capacete () no instante é:
Passo 4
Para finalizar, o exercício pede a diferença entre a velocidade da cabeça sem e com capacete (). Com os valores das velocidades em mãos, basta subtrair uma da outra: