Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo - Ex.

Quais são (a) a coordenada x e (b) a coordenada y do centro de massa da placa homogênea da Fig. 9-38 se L = 5,0   c m ?

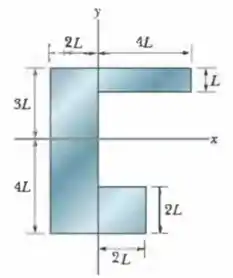
Passo 1

Vamos iniciar dividindo a placa em três partes:

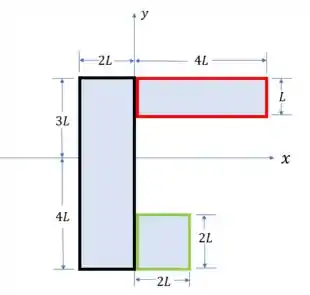
Já que essa placa toda é homogênea, a massa de cada uma das parte é proporcional a sua área, então para calcular o centro de massa da placa inteira, vamos usar os centros de massa das partes divididas através das seguintes relações:

x C M = A 1 x C M 1 + A 2 x C M 2 + A 3 x C M 3 A t o t a l

y C M = A 1 y C M 1 + A 2 y C M 2 + A 3 y C M 3 A t o t a l

Repara que ao invés de usarmos as massas, usamos as áreas, podemos fazer isso, pois a placa é homogênea!

Primeiro vamos calcular a área de cada parte dividida, sabendo que L=5:

A 1 = A p r e t o = 7 L * 2 L = 35 * 10 = 350

A 2 = A v e r m e l h o = 4 L * L = 20 * 5 = 100

A 3 = A v e r d e = 2 L * 2 L = 10 * 10 = 100

A t o t a l = A p r e t o + A v e r d e + A v e r m e l h o = 350 + 100 + 100 = 550   c m 2

Agora vamos calcular o centro de massa de cada área através das coordenadas do gráfico:

x C M 1 = - 2 L 2 = - L =   - 5

y C M 1 = - 4 L + 3 L 2 = - 0,5 L =   - 2,5

x C M 2 = 4 L 2 = 2 L = 10

y C M 2 = 3 L - 1 2 L = 2,5 L = 12,5

x C M 3 = 2 L 2 = L = 5

y C M 3 = - 2 L + ( - 2 2 L ) =   - 3 L = - 15

Passo 2

Portanto, usando a relação para determinar a coordenada x do centro de massa:

x C M = A 1 x C M 1 + A 2 x C M 2 + A 3 x C M 3 A t o t a l

x C M = 350 × - 5 + 100 × ( 10 ) + 100 × 5 550 =   - 0,455   c m

Passo 3

Agora, repetimos o procedimento para a coordenada y :

y C M = A 1 y C M 1 + A 2 y C M 2 + A 3 y C M 3 A t o t a l

y C M = 350 × - 0,5 × 5 + 100 × 2,5 × 5 + 100 × - 3 × 5 550 = - 2,05   c m

Resposta

  1. x C M = - 0,455   c m ;
  2. y C M = - 2,05   c m .
Ver Outros Exercícios desse livro