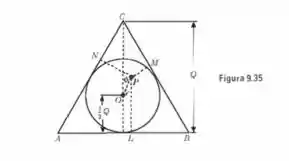
Uma bomba explode em três fragmentos de iguais massas m. A explosão liberta uma energia Q. Nesse caso, as leis de conservação da energia e da quantidade de movimento não determinam de modo único a energia e a quantidade de movimento de cada fragmento. Referindo o processo ao referencial C, mostre que (a) as energias cinéticas dos fragmentos podem ser representadas pelas distâncias de um ponto P aos lados de um triângulo equilátero de altura Q; (b) que a conservação da quantidade de movimento requer que o ponto P esteja dentro do círculo (de raio 1⁄2Q) inscrito no triângulo. Essa representação é chamada diagrama de Dalitz (Fig. 9.35) e é largamente usada para descrever a desintegração ele uma partícula fundamental em três fragmentos iguais.

Faala galera!!

Aqui, eu recomendo você reler a parte b do problema 9.13, nós usaremos algumas coisinhas que fizemos lá. De qualquer forma, vamos relembrar um pouco do que vale a pena:

Nós demonstramos que as partículas no momento da explosão têm o seu centro de massa relacionado ao momento e à velocidade no mesmo plano. Além disso, podemos assumir que as partículas se dirigem do ponto P da figura até M, N e L e, desta forma, no sistema C, como no problema 9.13. Assim, temos que:

A partir disso, conseguimos provar que:

, o que coincide com o que havíamos encontrar anteriormente!