O cabo do elevador de da Fig. 8-54 se rompe quando o elevador está parado no primeiro andar, onde o piso se encontra a uma distância acima de uma mola de constante elástica . Um dispositivo de segurança prende o elevador aos trilhos laterais, de modo que uma força de atrito constante de passa a se opor ao movimento. (a) Determine a velocidade do elevador no momento em que se choca com a mola. (b) Determine a máxima redução do comprimento da mola (a força de atrito continua a agir enquanto a mola está sendo comprimida). (c) Determine a distância que o elevador sobe de volta no poço. (d ) Usando a lei de conservação da energia, determine a distância total aproximada que o elevador percorre antes de parar. (Suponha que a força de atrito sobre o elevador seja desprezível quando o elevador está parado.)
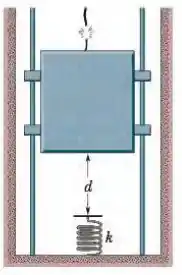
Figura 8-54 Problema 63.
Passo 1
a) A lei da conservação de energia pode ser escrita da seguinte forma
Neste caso sabemos que , logo:
No instante inicial, o elevador está parado (). Vamos tomar como referência o ponto mais alto da mola relaxada. Nesse caso temos (energia potencial gravitacional inicial) e o final da mola para (energia potencial gravitacional final). Temos que e logo:
Nesse caso o trabalho realizado sobre o sistema é o trabalho do atrito que é dado por
O sinal de menos aparece por que o atrito tira energia do sistema!
Substituindo os valores para , , e , temos:
Passo 2
b) Aplicando a lei de conservação de energia no instante que o elevador encosta na mola e quando a mola é comprimida de metros, temos:
Quando o elevador encosta na mola, há apenas energia cinética. No instante em que a mola é comprimida, temos uma energia potencial gravitacional (onde , pois se trata da compressão da mola) e uma energia potencial elástica além disso parte dessa energia inicial é dissipada pelo atrito, logo
Temos uma equação do 2° grau em função de , logo
Com
,
.
Para , ,, e
Substituindo os valores na fórmula de Bhaskara para encontrar o valor de x temos:
Passo 3
c) Queremos descobrir a distância que o elevador sobe de volta no poço. Vamos adotando como referência para energia potencial inicial o ponto mais baixo atingido pelo elevador, temos pela lei da conservação de energia que:
Passo 4
d) Na posição final, as forças agindo sobre o elevador entram em equilíbrio.
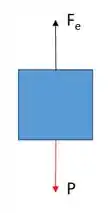
Vamos calcular o valor da variação sofrida na mola () no ponto de equilíbrio:
A energia dissipada pelo atrito é que determina a distância total percorrida pelo elevador, logo
Onde é a distância total.
Usando o ponto de equilíbrio como referência para a energia potencial gravitacional e aplicando a lei de conservação da energia temos que:
Resposta
a)
b)
c)
d)