Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo - Ex.
Um caixote de é arrastado sobre um piso, puxado por uma corda inclinada acima da horizontal. (a) Se o coeficiente de atrito estático é , qual é o valor mínimo do módulo da força para que o caixote comece a se mover? (b) Se , qual é o módulo da aceleração inicial do caixote?
Passo 1
Então galera , a primeira coisa que devemos fazer é construir o diagrama de corpo livre do caixote
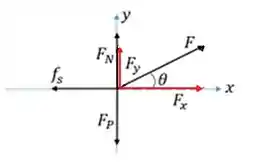
Vamos dar nomes as componentes da força F, a componente do eixo y é e a componente do eixo x é
Item (a).
Queremos descobrir o valor mínimo do módulo da força para que o caixote comece a se mover, para isso vamos considerar que o bloco não está em movimento e usar o coeficiente de atrito estático.
Sabemos que , logo:
Vamos aplicar a segunda lei de Newton para o eixo x, considerando que o bloco não está em movimento, logo a força resultante é zero:
Agora aplicamos a segunda lei de Newton para o eixo y, novamente o bloco não está em movimento então a força resultante é zero:
Sabemos que: e , logo :
Substituindo na equação do eixo y temos:
Podemos colocar F em evidência e isolá-lo :
Vamos substituir os valores que conhecemos:
Logo o valor mínimo do módulo da força para que o caixote comece a se mover é 304,5N
Passo 2
Item (b)
Queremos descobrir a aceleração do caixote, vamos considerar que há movimento no bloco e o coeficiente de atrito dinâmico.
Vamos aplicar a segunda lei de Newton para o eixo x
Sabemos que , então:
Agora aplicamos a segunda lei de Newton para o eixo y, novamente o bloco não está em movimento então a força resultante é zero:
Vamos substituir o valor de na equação anterior para descobrir a aceleração:
Podemos colocar o F em evidência:
Agora vamos substituir os valores conhecidos:
Resposta
(a)
(b)