Você deve executar quatro deslocamentos sucessivos na superfície plana num deserto, começando na origem de um sistema de coordenadas e terminando nas coordenadas . As componentes dos seus deslocamentos são, respectivamente, as seguintes, em metros: , , e . Determine (a) e . Determine (c) o módulo e (d) o ângulo (em relação ao semieixo positivo) do deslocamento total.
Passo 1
Este é um problema de soma vetorial utilizando componentes. Para resolver este tipo de questão precisamos ter em mente que:
Portanto, podemos somar indivualmente cada componente.
Passo 2
Como a superfície do deserto inicialmente está na origem e ocorre sucessivos deslocamentos, vamos realizar a soma individualmente dos componentes do deslocamento total, cujo o resultado final foi dado, portanto:
Para o eixo temos:
Isolando o
Passo 3
Seguindo o mesmo racíocionio, porém agora para o eixo , temos:
Isolando o :
Passo 4
Para calcular o módulo do vetor resultante aplicaremos a definição de módulo:
Passo 5
Para calcular a direção vamos iniciar ilustrando um triângulo retângulo cujo os catetos são as componentes e a hipotenusa é o módulo do vetor:
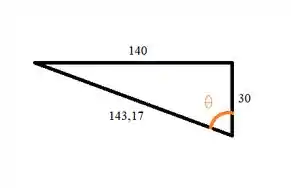
Aplicando a definição do cosseno:
Substituindo os valores:
Isolando o :
Como ele pede o ângulo que o vetor faz com o semieixo positivo de , precisamos somar a este ângulo , pois fizemos o calculo do ângulo do semieixo positivo de para o vetor. Portanto: