Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alonso e Finn - Campos e Ondas- Ed: 2º - Capítulo 14.Problemas - Ex. 89

Calcule a energia dos primeiros quatro estados estacionários de H e de H e + . Encontre, em cada caso, a energia necessária para elevar o sistema, do estado fundamental ao primeiro estado excitado. Represente as energias em uma escala por meio de linhas horizontais apropriadamente espaçadas. Observe que algumas energias coincidem. É possível deduzir uma regra geral?

Passo 1

Opaa tudo certo?

Vamos treinar mais um pouco dos conceitos aprendidos no capítulo!

Passo 2

O problema anterior nos dá a relação para cálculo de energia:

E n = - m e e 4 Z 2 8 ε 0 2 h 2 n 2

E como escrevemos comumente é:

E n = - R 2 h 2 c n 2

Onde:

  • h = 2 h h - → h - = 6,6207 ⋅ 10 - 34   m 2 ⋅ k g / s é a constante de Plank
  • ε 0 = 8,85 ⋅ 10 - 12 C 2 N ⋅ m 2 → constante de permissividade
  • m e = 9,1091 ⋅ 10 - 31   k g → massa de uma unidade de elétron
  • e = 1,6021 ⋅ 10 - 19 C → carga fundamental

Passo 3

Resolvendo para H :

E 1 = - 13,59   e V

E 2 = - 3,39   e V

E 3 = - 1,51   e V

E 4 = - 0,84   e V

E para H e + :

E 1 = - 54,39   e V

E 2 = - 13,59   e V

E 3 = - 6,04   e V

E 4 = - 3,39   e V

Passo 4

Plotando um gráfico para esses resultados temos as seguintes curvas:

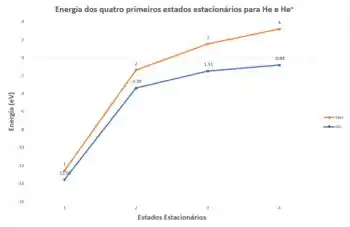
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro