Calcule o valor esperado de e o valor esperado de para a partícula associada à função de onda do problema 10.
Passo 1
Fala galerinha, beleza?
A função de onda fornecida pelo problema 10 é
Para calcular o valor esperado de , basta lembrar que
Para isso, fazemos
Observe que na substituição de tivemos que trocar o por . Assim,
O valor esperado será a integral dessa expressão:
Como é uma função par e é uma função ímpar, o integrando é uma função ímpar (o produto de uma função par com uma ímpar é uma função ímpar). Como a integral de uma função ímpar em um intervalo simétrico é nula, temos
Passo 2
Já para o valor esperado de , temos
Essa integral não se anula pois tanto o como são funções pares, de modo que o integrando é par.
Vamos fazer uma mudança de variável:
Assim,
Como o integrando é par, podemos fazer
Assim,
Passo 3
Essa integral não é muito difícil de calcular, só é um pouco chata. Você precisa aplicar integração por partes duas vezes. Suponho que você que esteja estudando quântica já domine esse tipo de integral, então vou recorrer ao WOLFRAM para obter o resultado. Procure no google ‘wolfram’ e na página inicial insira o seguinte o comando:
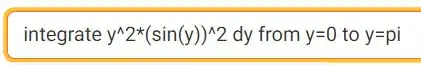
Ele vai te devolver o resultado da integral:
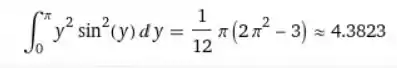
Assim,
Ou ainda,