Calcule os valores médios das energias cinética e potencial, no movimento harmônico simples, em relação (a) ao tempo, (b) à posição.
Passo 1
Faaala, galera!!! A força restauradora que atua sobre uma partícula que possui movimento harmônico simples é uma força conservativa. Considere o trabalho desta força sobre uma partícula de massa m no deslocamento de um ponto A de coordenada x1 até outro ponto B de coordenada x2 e depois na volta de B até A. O trabalho total realizado pela força é:
A energia potencial em um ponto de coordenada x, associada à força, quando o nível zero é tomado no ponto de coordenada x0 em que F=0, é:
Passo 2
Se fizermos a origem do sistema de coordenadas cartesianas coincidir com o nível zero de energia potencial, a energia potencial no ponto de coordenadas x fica:
Essa expressão nos dá a energia potencial em função da posição do oscilador. A energia potencial também pode ser expressa em função do tempo, com a equação de movimento. Lembrando que:
Passo 3
Temos que:
Além disso, o valor máximo da energia potencial é dado em:
Passo 4
A energia cinética do oscilador é obtida com a expressão da sua velocidade em função do tempo:
Podemos escrever a energia cinética em função da constante k:
E seu valor máximo é:
, e ocorre quando a partícula está em sua posição de equilíbrio.
Passo 5
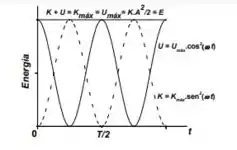
Gráfico das energias cinética, potencial e total em função do tempo;
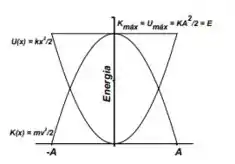
Energias cinética, potencial e total em função do deslocamento.
Resposta
Ei, a resposta está no passo a passo :)